Uma partícula de massa amarrada a um barbante de massa desprezível gira sobre uma mesa sem atrito, percorrendo uma circunferência de raio em torno do ponto . A pessoa que segura o barbante diminui lentamente o raio da circunferência até que .
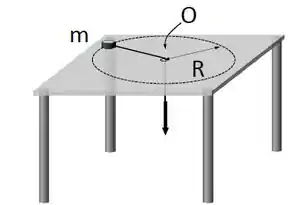
Se a velocidade angular inicial da partícula, sua velocidade angular final é:
(A)
(B)
(C)
(D)
(E)
(F)
(G)
(H)
Passo 1
Cara, se você estiver assustado com essa questão, pode relaxar! Ela é tranquilona...vem comigo:
Quando o momento angular de algum sistema se conserva?
Quando a soma de todos os torques externos a esse sistema é zero!!!!
Bem, tem alguma coisa externa ao nosso sistema partícula+mesa+barbante que esteja exercendo uma rotação ali na partícula? Não!!! Então o momento angular se conserva!!!
Esse produto vetorial fica fácil se a gente desenhar:
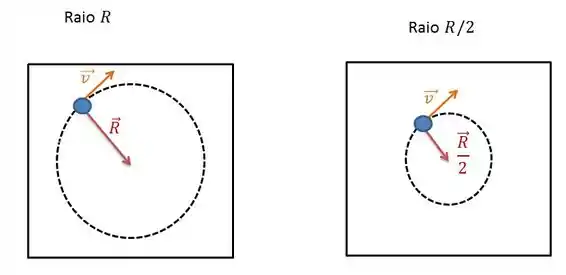
O ângulo entre o raio e a velocidade é então, calculando o módulo do momento angular:
Cortando o R.
Cortando o E usando que :
O enunciado fala que . Então:
A nossa alternativa correta é letra H.
Passo 2
Resposta
Alternativa correta é H.