Uma roda de massa e raio rola sem deslizar sobre uma superfície horizontal com
atrito ao ser puxada por uma força, aplicada sobreo seu eixo. O coeficiente de atrito entre a roda e a superfície é , e a velocidade do centro de massa é. O momento de inércia total da roda éem torno do eixo que passa pelo seu centro de massa.
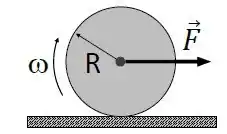
Julgue as seguintes assertivas
I. Na ausência de deslizamento, .
II. A energia cinética total da roda é.
III. Quando a força , é constante e a força de atrito é nula.
É correto apenas o que se afirma em
(A) I
(B) II
(C) III
(D) I e II
(E) I e III
(F) II e III
(G) Todas
(H) Nenhuma
Passo 1
1)
Rola sem deslizar????Como assim??

Relaxa!!! vou te explicar:
Isso quer dizer que agora estamos juntando translação e rotação... A velocidade no ponto de contato entre a roda e a superfície é zero...Não há dissipação de energia mecânica pela força de atrito!!!
E olha só, a cada ponto na roda de raio R que tá girando em uma velocidade angular , uma velocidade linear .
E se o centro de massa também translada, com uma velocidade , então cada ponto da roda, que falamos antes, tem uma velocidade
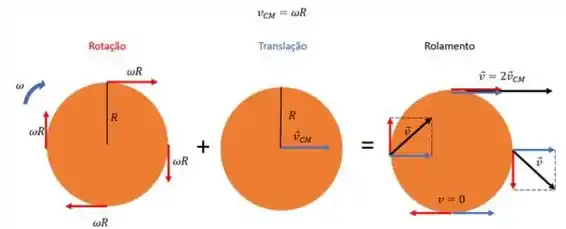
E aí? Show? Tá aliviado?

Então vamos ver essas afirmações.
Passo 2
Vamos ver essas afirmativas aí:
I) A gente acabou de falar ali no passo 1!
Quando não temos deslizamento, o vínculo é válido!!
Verdadeira
Passo 3
II) Temos translação e rotação , então:
Verdade!!
Passo 4
III)
Outra consequência de rolar sem deslizar é que a força de atrito é nula!! Porque a velocidade no ponto entre a superfície e a roda é zero constantemente, ou seja, a aceleração é nula, logo, pela segunda lei de newton, a resultante das força na horizontal é zero, e na horizontal tem a e , então ela é zero!
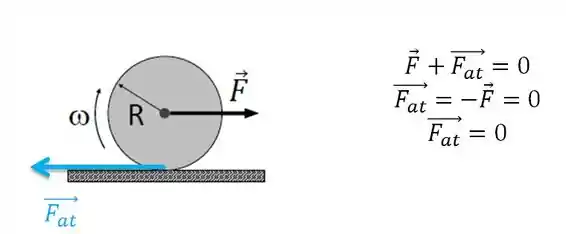
Verdade!!!
Então:
Alternativa G
Passo 5
Resposta
1) G