Três partículas de massa estão presas a hastes de tamanho e massas desprezíveis, como uma hélice. O sistema pode girar em torno de um eixo fixo que passa pelo seu centro, , e inicialmente possui velocidade angular . Um chiclete de massa incide com velocidade conforme a figura, e realiza uma colisão perfeitamente inelástica com uma das massas .
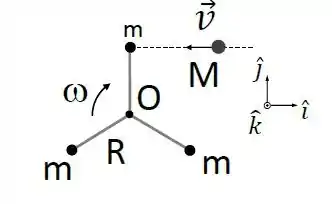
Julgue as seguintes assertivas
I. O momento de inércia do sistema composto pelas 3 massas é em relação ao eixo de rotação.
II. O momento angular inicial do sistema composto pelas 3 massas m aponta na direçãoem relação ao eixo de rotação.
III. O momento angular da massa antes da colisão tem módulo em relação ao eixo de rotação.
Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).
(A) I
(B) II
(C) III
(D) I e II
(E) I e III
(F) II e III
(G) Todas
(H) Nenhuma
Passo 1
Questão 1)
Fala aí!!! Vamos ver o que essa questão tá pedindo pra gente.
Temos um sistema que gira e uma colisão ali..mas nada de pânico...fica suave!
Vamos analisar as afirmações:
I) As hastes não tem massa, então é como se tivéssemos somente as bolinhas. Elas não tem raio, então pra gente calcular o momento de inércia desse sistema de três bolinhas é só usar a relação
Então essa é verdadeira!
Passo 2
II) Momento angular pode ser calculado de duas formas:
. Olha pre primeira igualdade, sabemos que o é um escalar, o é um vetor, então pra a igualdade ser verdadeira o tem que ter a mesma direção do . Sacou?
Ah beleza… Mas eu não sei a direção do ….
Regra da mão direita!! Olha aí, se o tá pra cima, então o momento angular também!!
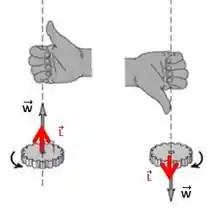
Fazendo isso, o nosso dedão tá apontando pra .
Logo também.
Assim essa afirmativa é Falsa
Passo 3
III)
Opaaaa olha pro que a gente escreveu ali em cima! Vamos usar agora a segunda igualdade:
, então o módulo disso é
Verdadeira!!!
Show??
Então a nossa alternativa é a letra E
Passo 4
Resposta
1) E