Um pequeno bloco de massa parte do repouso e desliza para baixo numa superfície curva sem atrito a partir de uma altura e depois adere a uma barra homogênea de massa e comprimento . A barra, inicialmente em repouso na vertical, então gira sem atrito em torno do eixo fixo de um ângulo antes de parar momentaneamente.
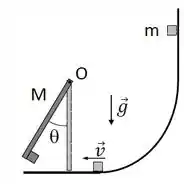
(A) Determine a velocidade do bloco após descer a superfície curva.
(B) Calcule o módulo do momento angular da massa em relação ao ponto , imediatamente antes do choque com a barra.
(C) Calcule o momento de inércia do conjunto barra + bloco em relação ao ponto .
(D) Calcule a velocidade angular do conjunto barra + bloco imediatamente depois do choque.
Dado: o momento de inércia de uma barra delgada de comprimento e massa girando sobre um eixo perpendicular à barra, passando por seu centro de massa é.
Passo 1
(A)
Bom, a superfície não tem atrito, ou seja, não temos forças dissipativas roubando energia do nosso sistema. Assim, a energia mecânica se conserva!
Conservando a energia entre os pontos 1 e 2:
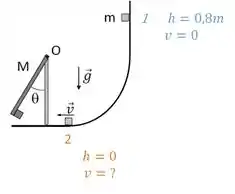
Beleza? Vamos pra próxima então.
Passo 2
(B)
Olha, o bloco adere a barra e depois eles giram, certo? Bom se tem alguma coisa girando, então tem um momento angular ali.
Como ele quer o módulo do momento angular antes da colisão:
Onde esse é a distância entre o bloco e o eixo .
No nosso caso, esse vale , que é o comprimento da barra.
E essa velocidade ai? Ele não fala no enunciado.
Mas a gente acabou de descobrir na letra (A), e vale .
Então substituindo os valores:
Só sucesso?
Passo 3
(C)
O momento de inércia pode ser calculado de duas formas diferentes. Uma é quando é para objetos “pontuais”, ou seja, considerados como partículas. Aí a fórmula é:
E o é a distância entre a partícula e o eixo de rotação.
A outra forma é quando o corpo é extenso, ou seja, quando a massa não tá concentrada em um pontinho só. Mas é tranquilo, porque, nesse caso, o momento de inércia é dado no exercício. Mas toma cuidado! Geralmente o valor dado é em relação a um eixo que passa pelo centro de massa do corpo. Se você tiver um eixo que não está passando pelo CM, aí tem que usar o teorema dos eixos paralelos!
Mas relaxa aí! Vamos por partes, que vai ficar mais simples!
A gente quer o momento de inércia do conjunto bloco+barra.
Vamos fazer um de cada vez:
Passo 4
Para o
A massa tá concentrada em um ponto, nota que o enunciado não fornece as dimensões do bloquinho.
Então estamos falando do primeiro caso do passo 3:
A distância que o bloco está do eixo vale
Show! Metade já foi. Vamos por
Passo 5
Agora, temos uma barra com comprimento
Eita...A massa está distribuída por esse corpo, então estamos falando da segunda situação do passo 3. Acompanha comigo:
O enunciado nos dá isso aqui:
Mas olha pra cá agora:
O eixo de rotação está passando pelo CM da barra??Não!
Então temos que ajeitar isso! Aí a gente vai usar o teorema dos eixos paralelos, que diz o seguinte, pra gente achar o de um eixo diferente do eixo que passa pela centro de massa, temos que somar o com , onde é a massa do corpo, e é a distância entre o CM e o novo eixo. Então é isso aqui ó:
No nosso caso, o é isso ali que eu destaquei na figura e vale
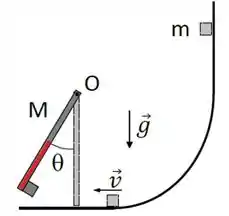
Maravilha!!
Então o
Passo 6
Vamos substituir isso tudo para achar o :
Suave??? Bora para o último!
Passo 7
(D)
Agora ele tá pedindo pra gente calcular a velocidade angular depois que o bloquinho grudou na barra.
Bem, eles vão girar, então vai ter um momento angular. Como não temos torques externos ao nosso sistema, o momento angular é conservado!
O a gente calculou lá na letra B, porque na ituação inicial o bloquinho tá na iminência de grudar na barra.
Então:
E o nosso é quando o bloco gruda na barra:
Da letra C:
Então:
Passo 8
Resposta
a)
b)
c)
d)