Uma partícula de massa amarrada a um barbante de massa desprezível gira sobre uma mesa sem atrito, percorrendo uma circunferência de raio em torno do ponto . A pessoa que segura o barbante diminui lentamente o raio da circunferência até que .
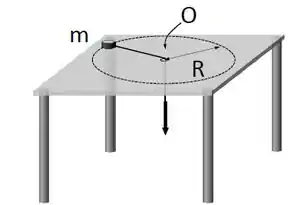
Considere as seguintes afirmativas relativas ao movimento da partícula:
I. O momento angular da partícula em relação a se conserva.
II. A velocidade angular da partícula em torno de aumenta.
III. O momento de inércia da partícula em relação a diminui.
É correto apenas o que se afirma em:
(A) I
(B) II
(C) III
(D) I e II
(E) I e III
(F) II e III
(G) Todas
(H) Nenhuma
Passo 1
Eita, esse enunciado parece difícil….mas só parece!! Vai ser moleza. Acompanha comigo, vamos analisar as afirmativas:
I) Quando o momento angular de algum sistema se conserva?
Quando a soma de todos os torques externos a esse sistema é zero!!!!
Bem, tem alguma coisa externa ao nosso sistema partícula+mesa+barbante que esteja exercendo uma rotação ali na partícula? Não!!! Então o momento angular se conserva!!!
Então essa afirmativa é verdade!!!

Passo 2
II) Olhando de cima da mesa, é isso o que tá acontecendo, certo?
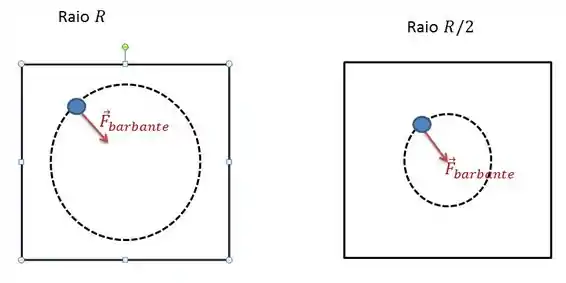
Bom, temos uma trajetória circular com uma força que aponta para o centro. Então:
Para a primeira situação, com o raio :
Para a segunda situação, com o raio :
Comparando as duas equações:
Portanto, com o raio menor, a velocidade angular é maior do que a velocidade angular com o raio maior!
Então essa afirmativa está correta!
Passo 3
III)
Opa! Ele quer informações sobre o momento de inércia da partícula, em relação ao eixo .
A gente sabe que:
Onde o é a distância da partícula ao eixo, beleza? No nosso caso é o raio da trajetória, mas esse raio tá diminuindo...E o é proporcional a , então de eu diminuir o raio, o momento de inércia também diminui!
Portanto, essa afirmativa é verdadeira!
Passo 4
Resposta
Alternativa G