Uma roda de massa e raio rola sem deslizar sobre uma superfície horizontal com
atrito ao ser puxada por uma força , aplicada sobreo seu eixo. O coeficiente de atrito entre a roda e a superfície é , e a velocidade do centro de massa é . O momento de inércia total da roda éem torno do eixo que passa pelo seu centro de massa.
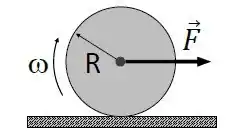
Considere que e . O maior valor do módulo da aceleração angular para o qual a roda não desliza é:
(A)
(B)
(C)
(D)
(E)
(F)
(G)
(H)
Passo 1
O que ele quer saber é, até qual valor da aceleração angular eu posso ter, sem ocorrer deslizamento.
Bom, como a gente descobre isso? Vamos analisar a situação de iminência de deslizamento, ou seja quando a força de atrito gerar um torque na roda. Ah, mas como estamos parados (iminência), o coeficiente de atrito é o estático, beleza?!
Calculando o torque
O módulo da normal é igual , confere?!
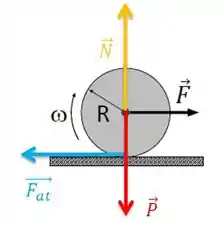
Como queremos o módulo disso, vemos a nossa alternativa certa é a letra D!!!
Showw! Suave na nave? De boa na lagoa?
Passo 2
Resposta
4) D