3º EE de Física 1 da UFPE - 2019.1

Uma partícula de massa kg move-se inicialmente com velocidade m/s em um plano horizontal sem atrito (ver Figura). Uma barra delgada e homogênea, de massa kg e comprimento m, repousa inicialmente sobre este mesmo plano. A barra pode girar sem atrito ao redor de um eixo fixo, perpendicular ao plano horizontal e que passa pelo ponto numa extremidade da barra. Em um dado instante, a partícula colide com o centro

da barra, perpendicularmente a ela, e fica grudada. O sistema barra + partícula passa então a girar ao redor do ponto .

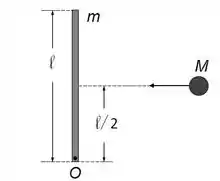
Qual é o momento de inércia da barra em relação a um eixo perpendicular a ela e que passa pelo ponto ? Dado: Momento de inércia da barra em relação a um eixo perpendicular a ela e que passa pelo seu centro de massa: .

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

Uma partícula de massa kg move-se inicialmente com velocidade m/s em um plano horizontal sem atrito (ver Figura). Uma barra delgada e homogênea, de massa kg e comprimento m, repousa inicialmente sobre este mesmo plano. A barra pode girar sem atrito ao redor de um eixo fixo, perpendicular ao plano horizontal e que passa pelo ponto numa extremidade da barra. Em um dado instante, a partícula colide com o centro

da barra, perpendicularmente a ela, e fica grudada. O sistema barra + partícula passa então a girar ao redor do ponto .

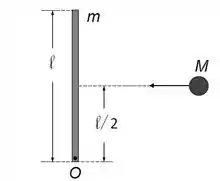
Considere as afirmativas abaixo a respeito da colisão entre a partícula e a barra:

(I) O momento linear total do sistema se conserva.

(II) A energia mecânica total do sistema se conserva.

(III) O momento angular total do sistema em relação ao ponto se conserva.

Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).

(a) I

(b) II

(c) III

(d) I e II

(e) I e III

(f) II e III

(g) Todas

(h) Nenhuma

Uma partícula de massa kg move-se inicialmente com velocidade m/s em um plano horizontal sem atrito (ver Figura). Uma barra delgada e homogênea, de massa kg e comprimento m, repousa inicialmente sobre este mesmo plano. A barra pode girar sem atrito ao redor de um eixo fixo, perpendicular ao plano horizontal e que passa pelo ponto numa extremidade da barra. Em um dado instante, a partícula colide com o centro

da barra, perpendicularmente a ela, e fica grudada. O sistema barra + partícula passa então a girar ao redor do ponto .

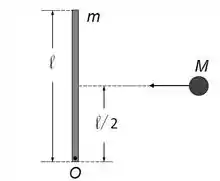
A velocidade angular do sistema barra + partícula imediatamente após a colisão é:

(a) 0 rad/s

(b) 1,2 rad/s

(c) 2,7 rad/s

(d) 3,6 rad/s

(e) 4,0 rad/s

(f) 4,8 rad/s

(g) 6,0 rad/s

(h) 7,2 rad/s

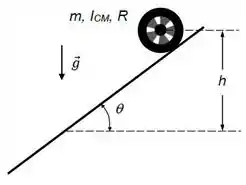
Uma roda possui massa , raio e momento de inércia em relação ao eixo perpendicular à sua superfície, passando pelo seu centro de massa (CM). Sabe-se que o CM da roda coincide com o seu centro. A roda rola sem deslizar sobre um plano inclinado de um ângulo com a horizontal (ver figura), onde e . Considere .

(A) Desenhe o diagrama de corpo isolado da roda, identificando cada força e o seu ponto de aplicação.

(B) Calcule a aceleração do CM da roda e a força de atrito que atua sobre ela.

(C) Calcule a velocidade do CM da roda após ela descer uma altura vertical ,

partindo do repouso.

(D) A força de atrito realiza trabalho ao longo dessa descida? Justifique sua resposta.

Uma partícula massiva encontra-se grudada em uma das extremidades de uma barra sem massa (ver Figura abaixo). A outra extremidade da barra está conectada na origem do plano horizontal . A partícula e a barra giram no plano , de modo que a partícula descreve uma circunferência com centro no ponto . A posição angular da partícula (em rad) é dada por:

onde o tempo é dado em segundos. O momento de inércia da partícula em relação ao eixo perpendicular ao plano e que passa no ponto é .

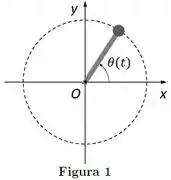
A energia cinética de rotação da partícula no instante vale:

(a) J (b) J (c) J (d) J (e) J (f) J (g) J (h) J

Uma partícula massiva encontra-se grudada em uma das extremidades de uma barra sem massa (ver Figura abaixo). A outra extremidade da barra está conectada na origem do plano horizontal . A partícula e a barra giram no plano , de modo que a partícula descreve uma circunferência com centro no ponto . A posição angular da partícula (em rad) é dada por:

onde o tempo é dado em segundos. O momento de inércia da partícula em relação ao eixo perpendicular ao plano e que passa no ponto é .

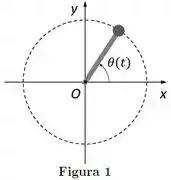
Qual é a aceleração centrípeta da partícula no instante inicial , sabendo que o raio da circunferência que ela descreve é ?

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

Uma partícula massiva encontra-se grudada em uma das extremidades de uma barra sem massa (ver Figura abaixo). A outra extremidade da barra está conectada na origem do plano horizontal . A partícula e a barra giram no plano , de modo que a partícula descreve uma circunferência com centro no ponto . A posição angular da partícula (em rad) é dada por:

onde o tempo é dado em segundos. O momento de inércia da partícula em relação ao eixo perpendicular ao plano e que passa no ponto é .

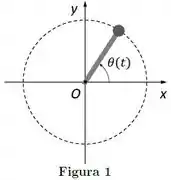
O módulo do torque resultante sobre a partícula em relação ao ponto no instante vale:

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)