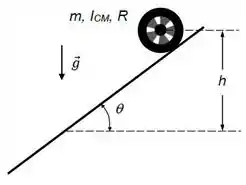
Uma roda possui massa , raio e momento de inércia em relação ao eixo perpendicular à sua superfície, passando pelo seu centro de massa (CM). Sabe-se que o CM da roda coincide com o seu centro. A roda rola sem deslizar sobre um plano inclinado de um ângulo com a horizontal (ver figura), onde e . Considere .

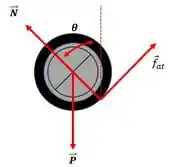
(A) Desenhe o diagrama de corpo isolado da roda, identificando cada força e o seu ponto de aplicação.

(B) Calcule a aceleração do CM da roda e a força de atrito que atua sobre ela.

(C) Calcule a velocidade do CM da roda após ela descer uma altura vertical ,

partindo do repouso.

(D) A força de atrito realiza trabalho ao longo dessa descida? Justifique sua resposta.

Item (B)

De acordo com a segunda Lei de Newton para forças e torques. Com relação à força, consideramos apenas a direção paralela ao plano.

(forças paralelas ao plano inclinado)

(torques em torno do centro de massa, onde é a aceleração instantânea)

Se

E

Substituindo o termo na primeira equação, temos:

Dessa maneira, isolamos em relação a e substituímos os valores:

Por fim, calculamos o valor da força de atrito:

Item (C)

Segundo a conservação de energia, temos:

Isolando a velocidade do CM e substituindo os valores, temos:

Item (D)

A força de atrito não realiza trabalho, devido ao fato de que não há deslizamento. Isto significa que não há deslocamento do ponto de contato da roda em relação ao ponto em que a força de atrito atua. Note que este fato é o que permitiu usar a conservação da energia no item (C). Caso houvesse deslizamento, haveria também perda de energia mecânica do sistema.