Uma partícula massiva encontra-se grudada em uma das extremidades de uma barra sem massa (ver Figura abaixo). A outra extremidade da barra está conectada na origem do plano horizontal . A partícula e a barra giram no plano , de modo que a partícula descreve uma circunferência com centro no ponto . A posição angular da partícula (em rad) é dada por:

onde o tempo é dado em segundos. O momento de inércia da partícula em relação ao eixo perpendicular ao plano e que passa no ponto é .

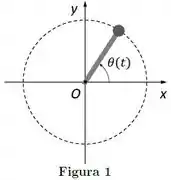
O módulo do torque resultante sobre a partícula em relação ao ponto no instante vale:

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

Dizemos que um corpo massivo possui aceleração angular quando a sua velocidade angular varia. Considerando que sabemos o conceito de velocidade angular instantânea (), a aceleração angular instantânea de um corpo massivo com velocidade angular variável pode ser calculada da seguinte forma:

Do mesmo modo, como , podemos expressar a aceleração angular como a derivada de segunda ordem da coordenada angular ():

Neste conteúdo, considerando um corpo rígido, o momento de inércia pode ser definido, de modo simples, como sendo a massa da partícula multiplicada pela distância ao eixo de rotação (raio):

Podemos descrever, para este caso, o torque de uma força aplicada em relação a um ponto com, a uma determinada distância , como:

Sabemos que a força é . Podemos considerar e . Logo, o torque angular resultante () para uma partícula massiva ou corpo rígido, pode ser calculado da seguinte forma:

Como , temos:

Agora que sabemos mais alguns conceitos, poderemos calcular o torque angular resultante () da partícula no instante .

Primeiro, calculamos a aceleração angular:

Sendo temos,

portanto o torque angular resultante é: