Exercícios Resolvidos de Teorema dos Eixos Paralelos

Exercício 10 1 2 3 4 5 6 7 8 9 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29

Enunciado

UFPE, Física 1, 2019.1, 3º EE, Questão 5

Uma partícula de massa kg move-se inicialmente com velocidade m/s em um plano horizontal sem atrito (ver Figura). Uma barra delgada e homogênea, de massa kg e comprimento m, repousa inicialmente sobre este mesmo plano. A barra pode girar sem atrito ao redor de um eixo fixo, perpendicular ao plano horizontal e que passa pelo ponto numa extremidade da barra. Em um dado instante, a partícula colide com o centro

da barra, perpendicularmente a ela, e fica grudada. O sistema barra + partícula passa então a girar ao redor do ponto .

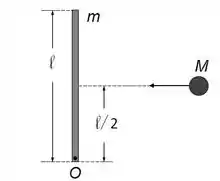
Qual é o momento de inércia da barra em relação a um eixo perpendicular a ela e que passa pelo ponto ? Dado: Momento de inércia da barra em relação a um eixo perpendicular a ela e que passa pelo seu centro de massa: .

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

Passo 1

Devemos calcular o momento de inércia da barra levando em consideração o teorema dos eixos paralelos. Nesse sentido, temos:

Momento de inércia da barra em relação ao eixo perpendicular a ela e que passa no centro de massa

Utilizando o teorema dos eixos paralelos temos:

Momento de inércia da barra em relação a um eixo perpendicular a ela e que passa pelo ponto

Resposta

Letra g.

Exercícios de Livros Relacionados

Calcule o momento de inércia de um aro (um anel fino) de raio R e massa M em relação a um eixo perpendicular ao plano do aro passando pela sua periferia.

Um disco uniforme de raio r e massa M gira em torno de um eixo horizontal paralelo ao seu eixo de simetria e que passa por um ponto de seu perímetro, de forma a poder oscilar livremente em um plano ve

Usando o teorema dos eixos paralelos e informações da Tabela 9.2, ache o momento de inércia da barra delgada de massa M e comprimento L indicado na Figura 9.23 em relação a um eixo passando pelo ponto

Uma barra delgada de comprimento L possui massa por unidade de comprimento variando a partir da extremidade esquerda, onde x = 0 , de acordo com d m / d x = γ x , onde γ é constante com unidades de k

Use a Equação (9.20) para calcular o momento de inércia de um disco maciço, uniforme, de raio R e massa M em relação a um eixo perpendicular ao plano do disco passando pelo seu centro.