UFPE, Física 1, 2019.1, 3º EE, Questão 6
Uma partícula de massa kg move-se inicialmente com velocidade m/s em um plano horizontal sem atrito (ver Figura). Uma barra delgada e homogênea, de massa kg e comprimento m, repousa inicialmente sobre este mesmo plano. A barra pode girar sem atrito ao redor de um eixo fixo, perpendicular ao plano horizontal e que passa pelo ponto numa extremidade da barra. Em um dado instante, a partícula colide com o centro
da barra, perpendicularmente a ela, e fica grudada. O sistema barra + partícula passa então a girar ao redor do ponto .
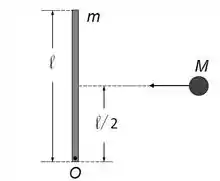
A velocidade angular do sistema barra + partícula imediatamente após a colisão é:
(a) 0 rad/s
(b) 1,2 rad/s
(c) 2,7 rad/s
(d) 3,6 rad/s
(e) 4,0 rad/s
(f) 4,8 rad/s
(g) 6,0 rad/s
(h) 7,2 rad/s
Passo 1
Primeiro, devemos calcular o momento angular inicial da partícula:
Onde, é a massa da partícula, a velocidade inicial, a distância do eixo ao ponto onde a partícula se alojou e o ângulo do impacto. Assim, temos:
Em seguida, calcularemos o momento angular final que é , onde é a soma das parcelas de momento de inércia da barra () e da partícula (). Portanto:
E
Agora, calcularemos a velocidade angular () com a seguinte relação (advinda da conservação do momento angular):
Resposta
Letra b.