Um canhão está preso na borda de um carrossel de raio que pode girar sem atrito sobre um eixo vertical fixo que passa pelo seu centro (ver Figura 2). O carrossel e o canhão têm um momento de inércia total em relação a esse eixo. O conjunto encontra-se inicialmente em repouso. O canhão então dispara uma bala de massa com uma velocidade tangencialmente ao carrossel. O conjunto carrossel + canhão passa a girar devido ao disparo.
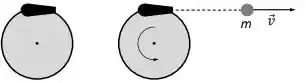
Após o disparo, qual é a velocidade angular do conjunto carrossel + canhão?
Passo 1
Bem... Sabemos do problema anterior que o momento angular se conserva, isto é, o momento inicial (antes de o canhão disparar) deve ser igual ao momento angular ...
Bem... Ta todo mundo parado inicialmente...

Portanto, o momento angular inicial é . Por consequência, o final também será.
Agora quem é o momento angular final?
É o momento angular da bala em relação ao centro de rotação do carrossel, somado com o momento angular do conjunto carrossel + canhão, ...
E é dessa relação que a gente vai por tirar a velocidade angular , já que o momento angular de um corpo que gira é .
Vamos ver isso com mais detalhes?
Passo 2
Cara, de acordo com a Teoria, o momento angular de um corpo com velocidade e uma distância do centro de rotação pode ser dado por...
Esse de fato é o momento angular da bola momentos depois dela sair do canhão (a distância dela ao eixo de giro do canhão de fato será , pois ela acabou se sair do canhão). O sinal de menos é só para indicar que a bola vai embora para a direita, saca?
Passo 3
Por outro lado, o momento angular do conjunto que entra em rotação pode ser dado por...
Onde é a velocidade angular do carrossel, justamente a velocidade pedida no problema, saca?
Como vimos no passo 1...
O problema nos deu a massa do canhão , , e , então...
Resposta
Letra C.