Uma esfera maciça e homogênea de massa e raio é mantida inicialmente em repouso sobre um plano inclinado de um ângulo (ver Figura 1). Quando liberada, a esfera passa a rolar sem deslizar plano abaixo.
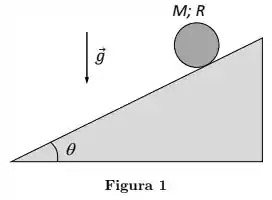
Considere as afirmativas abaixo sobre a situação em que a esfera já está em movimento:
- A força de atrito é nula.
- O trabalho da força de atrito é nulo.
- O torque da força de atrito em relação ao centro de massa da esfera é nulo.
Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).
- e
- e
- e
- Todas
- Nenhuma
Passo 1
Antes de julgarmos cada item, vamos fazer o digrama de forças no nosso desenho? Sempre é um bom começo, neh?
As forças que atuam na esfera nesse plano inclinado são: A força peso ...
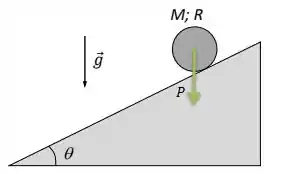
E também uma força de atrito contrária ao movimento circulatório...
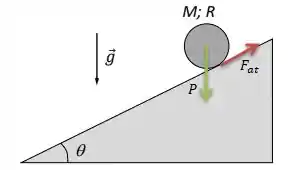
“AH! Mas como você sabe que tem força de atrito?”
Vou te responder isso, já julgando se o item é verdadeiro ou falso, bora lá?
Passo 2
ITEM I: A força de atrito é nula.
Cara... O problema deu a pista da existência da força de atrito quanto ele nos disse que a esfera gira sem deslizar. Se não fosse a força de atrito, a esfera escorregaria sobre o plano e não ia iniciar um movimento giratório, ta ligado?
Logo, esse item é falso.
Passo 3
ITEM II: O trabalho da força de atrito é nulo.
Cara... Para existir trabalho de alguma força qualquer, essa força tem que deslocar a massa do lugar em unidades. E se você observar, a velocidade do ponto que toca o chão da esfera, como ela não desliza, é sempre nula...
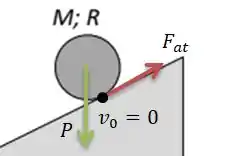
Isso significa que a força de atrito não desloca nada! Ela só faz girar . Logo, o seu trabalho de fato é igual a .
Passo 4
ITEM III: O torque da força de atrito em relação ao centro de massa da esfera é nulo.
ORA! Se a força de atrito é justamente a força que causa o giro dela, se não fosse a força de atrito ela nem giraria, então o torque dela tem que ser diferente de .
Item falso!
Resposta
Letra B.