Um canhão está preso na borda de um carrossel de raio que pode girar sem atrito sobre um eixo vertical fixo que passa pelo seu centro (ver Figura 2). O carrossel e o canhão têm um momento de inércia total em relação a esse eixo. O conjunto encontra-se inicialmente em repouso. O canhão então dispara uma bala de massa com uma velocidade tangencialmente ao carrossel. O conjunto carrossel + canhão passa a girar devido ao disparo.
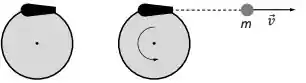
Considere o sistema formado pelo carrossel, canhão e bala. Sejam o momento linear total do sistema, o momento angular total do sistema em relação ao centro do carrossel e a energia mecânica total do sistema. No processo de disparo do canhão, é (são) conservado(s) apenas:
- e
- e
- e
- Nenhum
Passo 1
Cara! Pode anotar aí para qualquer questão de conservação que você pegar: momento linear , só se conserva se não tiver forças externas; momento angular se conserva se não tiver torque externo; e energia se conserva apenas se não tiver perdas.
Então bora analisar.
Passo 2
MOMENTO LINEAR .
Cara... Quando a bola do canhão está sendo expelida pelo canhão, a força da explosão surge nos dois sentidos pela 1ª lei de Newton: na bola, fazendo-a sair pela direita, e no canhão...
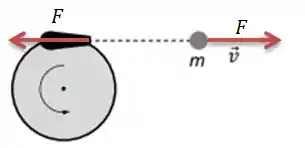
A força que surge no canhão tenderia a fazer o conjunto canhão+carrossel a se deslocarem para a esquerda. Todavia... Isso não acontece, já que o carrossel está fixado na parede e, portanto a parede faz uma força no sentido contrário a força no canhão...
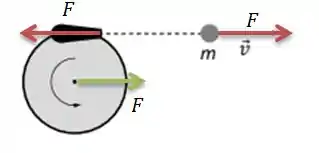
O que faz com que o conjunto carrossel+canhão não se desloque para a esquerda. Mas acontece que a parede não pertence ao sistema, logo a gente pode afirmar que uma força externa foi aplicada no sistema (a força da parede).
Segue então que se uma força externa foi aplicada ao sistema, o momento linear não se conserva.
Passo 3
MOMENTO ANGULAR .
Cara... Embora surja uma força externa na parada, veja que ela é uma força no centro de massa do carrossel que coincidentemente é o centro de rotação do mesmo. Isso significa que a única força externa que aparece não provoca nenhum torque externo no sistema.
Segue então que o momento angular se conserva.
Passo 4
ENERGIA MECÂNICA
Cara... Acabou de acontecer uma explosão. Com certeza se você encostar-se ao canhão você vai se queimar, pois explosão esquenta, neh? Isto prova que a energia mecânica não se conserva, pois parte dela se perde na explosão.
Segue que a energia mecânica não se conserva.
Resposta
Letra B