Um motor é ligado a um disco homogêneo de massa e raio (ver Figura 3). Em algumas situações, uma corda ideal enrolada no disco pode ser conectada a um bloco. A corda não desliza sobre o disco. Considere .
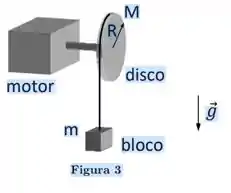
(A) (1,0 ponto) Suponha, inicialmente, a situação em que a corda ainda não esteja conectada ao bloco, ou seja, o bloco ainda não se encontra pendurado na figura ao lado. Nesse caso, a tensão na corda é nula. O motor aplica no disco um torque de módulo , em relação ao seu centro, que o faz girar. Escreva a equação de 2ª lei de Newton para o disco e determine a sua aceleração angular gerada por este torque.
Dado: Momento de inércia de um disco homogêneo de massa e raio em relação a um eixo perpendicular à sua superfície e passando no seu centro: .
(B) (1,5 ponto) Considere, agora, que um bloco de massa foi conectado à corda, como mostra a figura acima. Novamente, o motor aplica um torque , em relação ao centro do disco, que o faz girar, de modo que o bloco sobe verticalmente. Escreva as equações de 2ª lei de Newton para o disco e para o bloco.
(C) (1,5 ponto) Resolva o sistema de equações do item (B) e determine a aceleração angular do disco e a tensão na corda.
Passo 1
POW! Vamos imaginar ai o que está acontecendo nesse primeiro momento, beleza?
O problema nos disse que inicialmente não temos a massa conectada no disco...
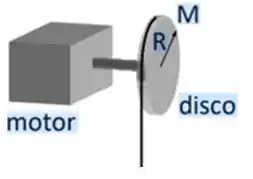
Relaxa que essa corda que fica é de peso desprezível ;). O que interessa é que você saiba que quando esse motor começa a girar, ele faz um torque no centro do disco que gera uma aceleração angular (o fazendo girar também). A equação que descreve isso é a equação de Newton para a rotação...
Onde é o momento de inércia do disco com relação ao eixo, saca? Repare que ela é bem parecida com a famosa equação: . A diferença é que estamos lidando com rotação, então ao invés de força , devemos falar em torque ;)
Para encontrar a aceleração angular então basta...
Então...
Onde é a massa do disco e é o seu raio. O problema nos deu essas informações então é só substituir mesmo...
Passo 2
Nesse caso já podemos e devemos considerar o bloquinho de massa ...
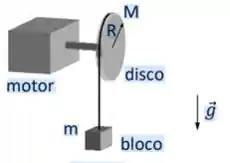
O problema quer agora que montemos as equações de Newton para o bloco e para o disco. Para isso, vamos antes de tudo desenhar o diagrama de forças nos objetos...
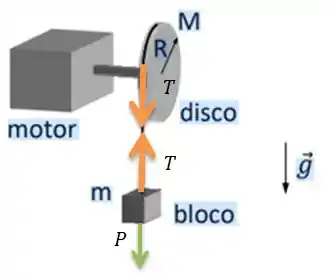
Repare que as forças estão todas aí: o peso do bloco e a tração na corda. Mas ainda está faltando uma coisa fundamental nesse desenho... O que é?
ORA! Está faltando representar também os torques. O motor faz um toque no disco de módulo , e a tração faz outro torque ...
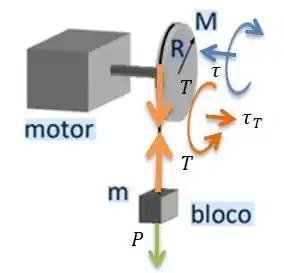
Com o diagrama completo, agora é só escrever as equações baseados na Lei de Newton! Vamos nessa?
Passo 3
Para o bloco, a Lei de Newton é a Lei normal: a soma das forças é igual a força resultante...
E a força resultante é ...
Onde é a aceleração do bloquinho.
O peso é dado por , então...
Passo 4
Para o disco...
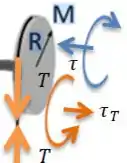
A soma dos torques tem que ser iguais ao torque resultante...
E o torque resultante é o momento de inércia vezes a aceleração angular ...
Só que o torque feito pela força de tração no eixo do cilindro pode ser obtido pelo...
Então...
Então está aí! As duas Leis de Newton para o conjunto bloquinho e cilindro é...
Passo 5
Agora é só meter bronca e resolver esse sistema!
Mas antes, tenha em mente que , a aceleração angular, sempre pode ser escrita em termos da aceleração tangencial (aceleração que a gente observa no bloquinho )...
Ao passo que também sabemos como se calcula o momento de inércia do disco...
Isolando em cima...
Substituindo em baixo...
Isolando ...
POW! Conhecemos todo mundo aí pelo enunciado!
Então...
Mas queremos a aceleração angular . Se lembrando de que ...
A tração agora ta fácil neh?
Resposta
Letra A:
Letra B:
Letra C: