Uma partícula de massa descreve uma trajetória na forma de uma circunferência de raio . Sua posição angular (em rad.) e dada pela expressão:
Com o tempo em segundos.
O módulo da aceleração tangencial da partícula (em ) no instante vale:
Passo 1
Bem... Como não veio desenhado para gente um esqueminha desse treco, que tal começarmos o problema nessa tarefa? Bora desenhar então!
O problema nos disse que temos uma bolinha de massa girando numa circunferência de raio
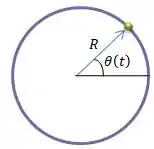
A posição angular dessa bolinha varia com o tempo de acordo com essa equação...
Repare que a partir dessa informação, podemos tirar vários insights sobre a partícula como a velocidade angular , ou até mesmo a aceleração angular .
No nosso caso, estamos buscando aqui a aceleração tangencial que pode ser dado por...
Então repare que temos que antes buscar . Vamos nessa?
Passo 2
Pow! Pela cinemática rotacional, sabemos que...
Onde é a velocidade angular que por sua vez é a derivada da posição angular...
Então...
Pegando esse resultado e derivando novamente mas dessa vez para determinar o valor de ...
No tempo ...
POW! Então o valor da aceleração tangencial nesse instante será...
Resposta
Letra A.