1º EE de Física 1 da UFPE - 2019.1

Dois carros (A e B) partem da mesma posição inicial em e movem-se em pistas retas paralelas. Seus gráficos da velocidade em função do tempo são mostrados na Figura 1.

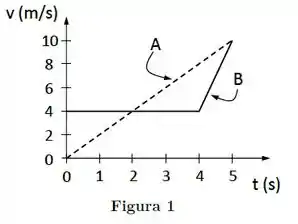
A distância entre os carros no instante é:

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

A posição de uma partícula em metros é descrita pelo vetor posição

O instante em que a partícula inverte o sentido do seu movimento é:

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

A posição de uma partícula em metros é descrita pelo vetor posição

Seja o ângulo em radianos que o vetor velocidade da partícula faz com o eixo no instante . Pode-se afirmar que é igual a:

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

Uma partícula de massa executa um MCU no sentido anti-horário com raio e período . O centro da sua trajetória coincide com a origem do sistema de coordenadas.

No instante , o vetor posição da partícula em metros é . No instante , a força centrípeta (em newtons) agindo na partícula é:

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

Dois carros (A e B) partem da mesma posição inicial em e movem-se em

pistas retas paralelas. Seus gráficos da velocidade em função do tempo são mostrados na Figura 1.

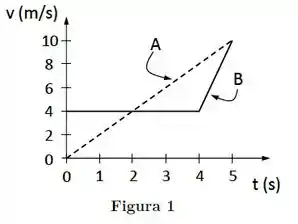
A velocidade média do carro B no intervalo entre e é:

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

Dois carros (A e B) partem da mesma posição inicial em e movem-se em

pistas retas paralelas. Seus gráficos da velocidade em função do tempo são mostrados na Figura 1.

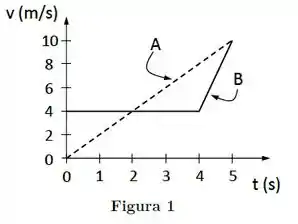
Considere as afirmativas abaixo:

(I) A variação da velocidade de B é maior que a de A no intervalo entre e .

(II) As acelerações de A e B são iguais no instante .

(III) A aceleração média no intervalo entre e é maior para A.

Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).

(a) I

(b) II

(c) III

(d) I e II

(e) I e III

(f) II e III

(g) Todas

(h) Nenhuma

A Figura 2 mostra um bloco de massa , inicialmente em repouso, em contato com uma parede vertical. Os coecientes de atrito estático e cinético entre o bloco e a parede são, respectivamente, e .

Uma força de módulo encontra-se aplicada ao bloco, fazendo um ângulo com a vertical. O ângulo é tal que

e . Considere a aceleração gravitacional de módulo .

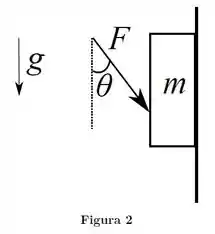
(a) Faça o diagrama de corpo livre do bloco, desenhando todas as forças que atuam sobre ele.

(b) Calcule o módulo da força normal que a parede exerce sobre o bloco.

(c) O bloco se move? Justique sua resposta.

(d) Calcule os módulos da força de atrito e da aceleração do bloco.