Trabalho e Energia Cinética
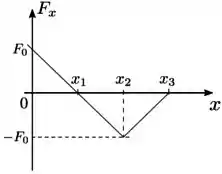
Uma partícula se desloca ao longo do eixo , da origem até a posição , onde é uma distância positiva. A única componente da força resultante sobre a partícula, , varia com a posição conforme o gráfico da figura, linearmete da origem a , cortando o eixo em , e também linearmente de até ; no gráfico também está indicado o valor máximo da força. Denotando por , , e as energias cinéticas nas posições , , e , respectivamente, podemos afirmar sobre as variações , e que
- e
Passo 1
O exercício pede a variação de energia cinética. Temos que lembrar duas coisa.
Lembra do teorema trabalho energia?
A outra coisa é que o trabalho se relaciona com a força por meio de
Como é uma integral, o trabalho também pode ser pensado como a área em baixo de um gráfico .
Juntando esses dois temos
As áreas no gráfico são triângulos, então é tranquilo de calcular a área \o/
OBS: É importante lembrar que a área abaixo do gráfico é negativa.
Passo 2
Vamos começar calculando (é a área de até )
Passo 3
Vamos calculando (é a área de até )
Aqui vamos ter dois triângulos (um pra cima e outro pra baixo)
Passo 4
Vamos começar calculando (é a área de até )
Aqui vamos ter três triângulos (um pra cima, dois pra baixo)
Passo 5
Então
Resposta
Letra B