Movimento Circular
Uma partícula em trajetória circular de raio tem um vetor aceleração que em um certo instante faz um ângulo com o vetor velocidade . Podemos afirmar que nesse instante
- O módulo da velocidade da partícula é igual a ;
- O módulo da velocidade da partícula é igual a ;
- A aceleração da partícula tem módulo ;
- O módulo da velocidade da partícula está aumentando;
- O módulo da velocidade da partícula está diminuindo;
Passo 1
No movimento circular, a velocidade é tangencial ao movimento.
Como a aceleração possui um ângulo de com a velocidade, significa que ela não é somente a aceleração centrípeta mas também tem a componente tangencial.
A aceleração tangencial é no mesmo sentido da velocidade isso porque o ângulo entre a velocidade e a aceleração é menor que .Vamos fazer um desenho para visualizar melhor.
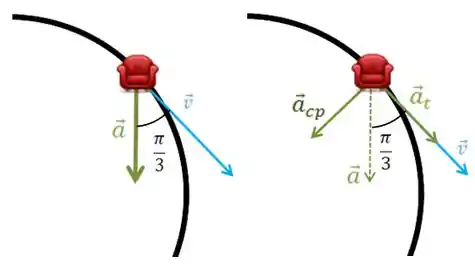
Repara no desenho, que a aceleração tangencial é no mesmo sentido que a velocidade então o módulo da velocidade está aumentando.
Resposta
Letra D
Exercícios de Livros Relacionados
Um ventilador realiza 1200 revoluções por minuto. Considere um ponto situado na extremidade de uma das pás, que descreve uma circunferência com 0,15m de raio. (a) Que distância o ponto percorre em uma
Um menino faz uma pedra descrever uma circunferência horizontal com 1,5m de raio e uma altura de 2,0m acima do chão. A corda arrebenta e a pedra é arremessada horizontalmente, chegando ao solo depois
Um relógio de parede tem um ponteiro de minutos com um comprimento de 0,50m e um ponteiro de horas com um comprimento de 0,25m . Tome o centro do relógio como a origem, e usa um sistema de coordenadas
No problema 38 , encontre os deslocamentos da ponta de cada ponteiro (ou seja Δ A → e Δ B → ) quando o tempo avança de 3 : 00P . M . para 6 : 00P . M .
Uma bola de baseball é lançada de forma que sua velocidade inicial ao perder contato com o taco faz um ângulo de 30 ° acima da horizontal. Ela deixa o taco a uma altura de 1,0m acima do solo e aterris