Um anel de massa , ligado a duas molas de constantes elásticas iguais a e , pode deslizar sem atrito sobre um trilho rígido horizontal, como mostra a figura, na qual está indicado um sistema de eixos , com na direção do trilho. Inicialmente o anel se encontrava em repouso sobre o trilho na posição onde as duas molas estão relaxadas. A partir do instante o anel passou a sofrer a ação de uma força constante , numa direção que faz um ângulo com a horizontal, levando o anel a oscilar em torno de um novo ponto de equilíbrio.

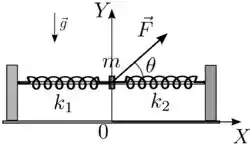
1. Qual a força total que o trilho exerce sobre o anel?
2. Em que posição é nula a resultante das forças que atuam sobre o anel?
3. Escreva a energia potencial elástica do sistema em função da coordenada do anel.
4. Escreva a energia potencial associada à força constante em função da coordenada do anel.
5. Expresse o módulo da velocidade do anel em função de sua coordenada .

a)

Vamos fazer o DCL do corpo. Vamos responder as perguntas do passo a passo para colocar as forças

1. A massa dele é considerada?

Sim, ele tem massa.

2. Ela esta encostada em alguma superfície?

Sim, o bloco está em contato com o trilho.

3. Tem algum fio?

Não, não existe um fio atuando.

4. Tem mola?

Sim, temos duas molas.

5. Tem atrito?

Não, não existe atrito.

O seu DCL fica

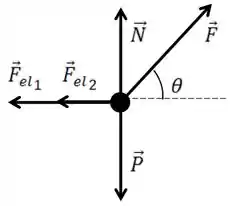
Tem um detalhe importante a se tocar, o sentido da força elástica. Eu a considerei para a esquerda porque estou considerando positivo, o que faz a mola ser apertada e a mola ser esticada, ambas querem voltar para o meio. Se estivéssemos considerando negativo o seu sentido vai ficar invertido.

Essa idéia do sinal da é bem complicada, mas podemos fazer dessa forma simplicada por enquanto.

Voltando ao DCL, vamos fazer o equilíbrio ao longo de isso porque queremos que está na vertical

Devemos encontrar usando a “regra do COlado, SEparado”.

b)

Para acharmos a posição que a força resultante é nula vamos fazer o equilíbrio no , o que muda é a deformação da mola. Como já vimos para o sentido da força elástica ser aquele o deve ser positivo. Como queremos o equilíbrio ela deve ser assim mesmo. Vamos ignorar isso por enquanto

Devemos encontrar usando a “regra do COlado, SEparado”.

c)

Teremos duas energias potenciais elásticas, da mola e da mola

Repara que dessa vez escrevi direto, porque já sabemos que a mola vai se deformar já que o zero é seu equilíbrio

d)

Considerando que a energia potencial associada a uma força pode se relacionar com o trabalho

Onde

Pela fórmula de trabalho. Se for negativo ele faz o trabalho ser negativo, isso vai de acordo com os sinais de trabalho que vimos no capitulo sobre isso.

Porque , então

e)

Repara que não temos força de atrito, então a energia mecânica se conserva

Onde é a energia mecânica em um ponto qualquer

A energia mecânica inicial é zero, isso porque as molas estão relaxadas, não temos velocidade, e o deslocamento em é zero. Alem disso, teremos

Então