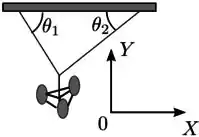
Um lustre é pendurado em um teto horizontal por dois fios, considerados ideais, que se juntam e são ligados ao lustre, como mostra a figura. Em um dos fios, que faz um ângulo de com o teto, a tensão tem módulo ; no outro, que faz um ângulo com o teto, a tensão tem módulo . Considerando o sistema de eixos com na vertical, como indicado na figura, obtemos que a razão entre as componentes verticais e das tensões é
- ;
- ;
- ;
- ;
- ;
Passo 1
Vamos começar o problema fazendo DCL do bloco
Temos os seguintes dados do enunciado
Em problemas literais é sempre bom escrever os dados separados para mais tarde conferir se as respostas estão de acordo com esses dados.
Vamos responder as perguntas do passo a passo para colocar as forças no DCL
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
Sim, ele tem massa.
Não, ele não está apoiado em nenhuma superfície.
Sim, existem dois fios atuando.
Não, não existe mola atuando.
O DCL do bloco fica
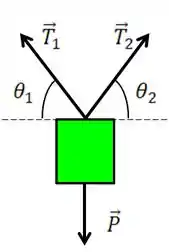
Repare que os ângulos dos fio são com a horizontal, na parte de baixo eles são os ângulos dos fios com a horizontal.
Passo 2
Para achar a razão entre as componentes verticais da tração, devemos achar e .
Vamos usar a regra do COlado, SEparado”, para achar a componente.
Então
Devemos achar
Passo 3
Vamos fazer a analise das forças no porque o bloco está em equilíbrio
Devemos encontrar e usando a “regra do COlado, SEparado”.
Então
Passo 4
Recapitulando,
Acabamos de achar , então
Jovem, você deve estar se perguntando como surgiu a tangente né?
É um pouco estranho ver, vou te explicar. Primeiro, sabe como eu sabia sem fazer conta que ia aparecer a tangente? Pelas alternativas da múltipla escolha!!
Nenhuma delas tinha mais de um ou .
Agora entendendo direitinho como apareceu a tangente,
Repara que eu só mudei a ordem da multiplicação. Você lembra de divisão de fração?
Você mantém a primeira e inverte a segunda.
Concorda comigo então que
Ficou confuso?
Eu só “desinverti” e coloquei uma divisão
Porque isso fica
Resposta
Letra C