Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Polias Não-Ideais

Ver Teoria
Exercício 3512345678910111213141516171819202122232425262728293031323334363738394041424344454647

Enunciado

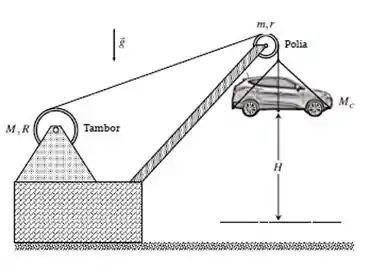
Em uma exposição para vendas, um carro de massa M c é mantido a uma certa altura do solo através de um cabo ligado a um guindaste. Em um dado instante a trava que mantém o carro elevado falha e ao mesmo tempo começa a cair, fazendo o cabo desenrolar do tambor (cilindro maciço de raio R e massa M ) e girar a polia superior de raio r e massa m .

Após cair por uma distância H o sistema de segurança da máquina é acionado, fazendo com que o carro pare. Durante a queda, pode-se desprezar deslizamentos no movimento do cabo pelo tambor e pela polia.

Responda as perguntas abaixo desprezando a massa do cabo e apresente as respostas em função de M c , M , m , R , r , H e g .

(a) Calcule o módulo da velocidade do carro no instante imediatamente anterior ao acionamento do sistema de segurança.

(b) Calcule o módulo da aceleração do carro durante sua queda

(c) Calcule o módulo da tensão no cabo no trecho entre o tambor e a polia durante a queda do carro

Passo 1

letra a)

Como não existe força externas atuando no sistema até ele parar pelo acionamento do sistema de segurança, podemos conservar a energia mecânica, ou seja:

E i = E f

Assim, calculando a energia em cada momento.

M c g H = 1 2 M c v c 2 + 1 2 I 1 ω 1 2 + 1 2 I 2 ω 2 2

Como as polias não são ideais, não podemos esquecer que elas também têm energia cinética. Vamos chamar de polia 1 a que fica na esquerda e a de polia 2 a que fica localizada na direita.

Além disso temos que perceber também que como um cabo está ligado tudo, tanto as polias quanto o carro, todos eles possuem a mesma velocidade linear, porque se um fosse mais rápido que o outro a corda arrebentaria!!!

ω 1 = v c R

ω 2 = v c r

Além disso vamos usar também a fórmula do momento de inércia de cada uma das polias

I 1 = 1 2 M R 2

I 2 = 1 2 m r 2

Calma, agora é só substituir tudo isso na equação que nós achamos de energia mecânica.

E i = E f

M c g H = 1 2 M c v c 2 + 1 2 1 2 M R 2 v c R 2 + 1 2 1 2 m r 2 v c r 2

M c g H = 1 4 2 M c + m + M v c 2

Isolando o v c

v c = 2 M c g H m + M + 2 M c

Passo 2

Letra b)

Primeiro vamos fazer achar todas as forças que estão atuando no sistema, pra depois nós começarmos a fazer a segunda lei de Newton em cada movimento.

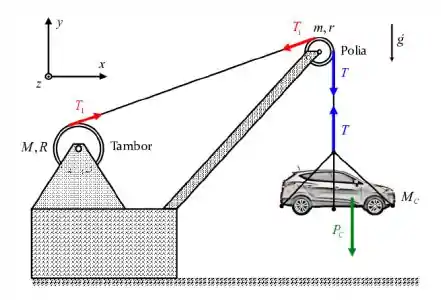
Assim, escrevendo a segunda lei de Newton pro carro ficamos com

M c a = M c g - T

a = g - T M c

Agora se a gente olhar pro tambor, podemos relacionar o torque com a aceleração angular dele

T R = I 1 α 1

R T 1 = I 1 α 1

T 1 = I 1 α 1 R

Agora olhando só pra polia, vamos poder relacionar as duas coisas. Vamos fazer do mesmo jeito que fizemos com o tambor.

T R = I 2 α 2

I 2 α 2 = r T 1 - T

T = T 1 + I 2 α 2 r

Agora que já escrevemos todas as equações precisamos fazer algumas substituições. Assim como nas alternativas anteriores nós relacionamos as velocidades lineares, aqui vamos relacionar as acelerações lineares também.

Assim como também vamos substituir os momentos de inércia, já que estamos calculando sempre em relação ao centro de rotação.

I 1 = 1 2 M R 2

I 2 = 1 2 m r 2

α 1 = a R

α 2 = a r

Substituindo isso nas equações que nós encontramos vamos ter que

T 1 = 1 2 M a

T = 1 2 M + m a

a = 2 M c m + M + 2 M c g

Oooooouuuuuu.... a gente pode aplicar o bom e velho Torricelli, já que a aceleração no carro é constante!

v c 2 = v 0 2 + 2 a H

Como a velocidade inicial é nula e já temos a velocidade v c , temos

v c 2 = 2 a H → a = v c 2 2 H

a = 1 2 H 4 M c g H m + M + 2 M c

O que dá o mesmo resultado (ainda bem!)

a = 2 M c m + M + 2 M c g

Passo 3

Depois que a gente fez a letra b essa aqui fica sendo só substituir o valor encontrado

Como achamos que

T 1 = 1 2 M a

a = 2 M c m + M + 2 M c g

Então chegamos na resposta

T 1 = M c m + M + 2 M c M g

Resposta

Letra a)

v c = 2 M c g H m + M + 2 M c

Letra b)

a = 2 M c m + M + 2 M c g

Letra c)

T 1 = M c m + M + 2 M c M g

Exercícios de Livros Relacionados

Um dispositivo para medir o momento de inércia de um corpo é mostrado na figura. A plataforma circular está presa a um tambor concêntrico de raio R , plataforma e tambor estando livres para girar em t
Um cilindro de uniforme, de massa M e raio R , tem um fio enrolado no seu entorno. O fio é mantido fixo, enquanto o cilindro cai verticalmente, como mostrado na figura. (a) Mostre que a aceleração do
A extremidade superior do fio enrolado em redor do cilindro da figura está segura por uma mão que acelera para cima, de modo que o centro de massa do cilindro não se move, enquanto o cilindro gira. De
Calcule o efeito da massa M da polia, de raio R , sobre o sistema do Cap. 4, Probl. 12 (fig); a masssa m , que desliza sem atrito está ligado à massa suspensa m ' pelo fio que passa sobre a polia. Det
Um bloco de massa m , que pode deslizar com atrito desprezível sobre um plano inclinado de inclinação θ em relação à horizontal, está ligado por um fio, que passa sobre uma polia de raio R e massa M ,