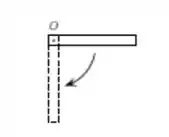
Uma barra uniforme de comprimento e massa está pressa por uma das extremidades a um pivot com atrito desprezível, e, livre para girar no plano vertical. A barra é liberada do repouso na posição horizontal como mostra a figura. Ao atingir a posição vertical, a velocidade linear da extremidade da barra oposta ao pino é

(a)

(b)

(c)

(d)

(e)

Conservando a energia mecânica do sistema temos que

Substituindo os valores do problema ficamos com

Ok...mas por que ???

Precisamos da energia potencial gravitacional do centro de massa, certo? Se considerarmos o nível “zero” de energia a posição do centro de massa quando a barra está na vertical, percebemos que o valor inicial da energia potencial gravitacional da barra (quando ela está na horizontal) é

Agora vamos ter que substituir aquele usando o teorema dos eixos parelelos, já que só conhecemos o eixo que passa pelo centro da barra

Isolando a velocidade temos que

Porém essa é a velocidade angular do centro de massa da barra, como queremos a extremidade temos que fazer uma alteração ainda, e não se esquecer que ele pediu a velocidade linear