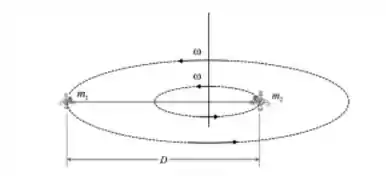
Após um acidente, dois astronautas se encontram isolados no espaço, ligados por um cabo esticado de comprimento , e, girando com velocidade angular em relação a um eixo ortogonal ao cabo e que passa pelo centro de massa do sistema formado por eles (ver figura). Podemos considerar que as dimensões dos astronautas são muito menores que a extensão do cabo e, trata-los como se fossem duas partículas. Sabendo que os dois astronautas têm massas relacionadas por , calcule o raio da trajetória circular do astronauta de massa
a)
b)
c)
d)
e)
Passo 1
Como eles estão ligados por um cabo, temos que os dois possuem a mesma força centrípeta, logo.
Porém como foi dado no problema
Assim
Como a distância do cabo é
Sendo assim, como ele quer saber