ENUNCIADO A: Após um acidente, dois astronautas se encontram isolados no espaço, ligados por um cabo esticado de comprimento , e, girando com velocidade angular em relação a um eixo ortogonal ao cabo e que passa pelo centro de massa do sistema formado por eles (ver figura). Podemos considerar que as dimensões dos astronautas são muito menores que a extensão do cabo e, trata-los como se fossem duas partículas
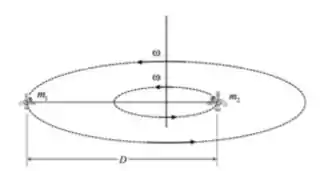
Considere o problema apresentado ENUNCIADO A. Em um dado instante, os dois astronautas começam a se aproximar puxando o cabo. Das afirmações abaixo, assinale aquelas que são corretas.
(I) O momento de inércia de cada astronauta em relação ao eixo de rotação é tal que
(II) O momento angular do sistema em relação ao eixo apresentado se manterá constante
(III) Quando a distância entre os astronautas tiver sido reduzida pela metade a velocidade angular deles será .
- Todas as afirmações são corretas
- Apenas (I) e (II)
- Apenas (I)
- Apenas (III)
- Apenas (II) e (III)
Passo 1
Afirmação 1 – Verdadeira
o momento de inércia pode ser dado como
E como podemos notar na figura, a distância do astronauta 1 do centro é maior que a distância do astronauta 2 do centro. Assim:
Logo:
Passo 2
Afirmativa 2 - Verdadeira
Como não há torque externo no sistema, o momento angular irá permanecer constante.
A única troca de forças que existe é interna ao sistema, ou seja, não há alteração do momento angular quando os astronautas puxam a corda.
Passo 3
Afirmativa 3 – Verdadeira
Conservando o momento angular teremos que