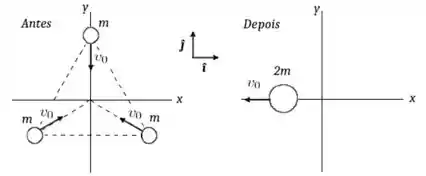
Três átomos idênticos de massa se deslocam no plano horizontal com velocidade de mesmo módulo , de tal forma que os três colidem num determinado ponto. Antes da colisão, os átomos encontram-se sempre equidistantes um do outro conforme mostra a figura. Após a colisão, verifica-se que dois dos átomos formam uma molécula de massa , que se move ao longo do sentido negativo do eixo , com uma velocidade de modulo . O terceiro átomo move-se isoladamente após a colisão. Responda as questões abaixo usando como dados e .

A) Mostre que a velocidade do centro de massa do sistema formado pelos três átomos é nula.

B) Calcule o vetor velocidade do terceiro átomo após a colisão no sistema de coordenadas indicado na figura.

C) Calcule a variação da energia cinética do sistema devido à colisão.

Letra b)

Como na colisão não há ação de forças externas, podemos conserva o momento linear antes e depois do choque entre os átomos.

Calculando os momentos

Como vimos na questão anterior, a soma das velocidades inicias é 0, sendo assim

Então ..

Agora vamos calcular o momento final

Não se esqueça dos vetores unitários!! Eles são muito importantes e o IF realmente tira pontos se esquecer deles

Letra c)

Para calcular a variação de energia cinética é só calcular a energia cinética de cada átomo antes e depois.

Isso vai dar bem bonito porque alguns termos que poderiam atrapalhar a conta que vão aparecer no segundo termo irão sumir com os que estão no terceiro termo.

Arrumando a casa a gente fica com isso

Agora vamos calcular a energia cinética depois

Agora pra calcular a variação de energia é só diminuir uma da outra