Listas Física 1 - UFSCAR de Física 1 da UFSCAR - Lista 2 - Dinâmica
Física 1 - UFSCAR
Uma ou duas forças agem sobre um disco metálico que se move sobre o gelo sem atrito ao longo do eixo , em movimento unidimensional. A massa do disco é . As forças , para direita, e , para esquerda, atuam ao longo do eixo e tem módulos e . Uma força faz um ângulo de com o eixo e tem módulo . Qual é a aceleração do disco quando apenas a força atua? Quando as forças e agem? E com todas as forças atuando sobre o disco?
Ver solução completaUma partícula de massa está se movendo sobre atuação de uma força que depende de sua velocidade. A força é dada por:
onde e são constantes positivas e é a magnitude da velocidade da partícula. Se no tempo , a partícula está se movendo a uma velocidade de magnitude descubra a função da magnitude da velocidade com o tempo. Use as constantes mencionadas no problema. Supondo que a equação adote o Sistema Internacional de unidades, qual seria as unidades das constantes e variáveis mencionadas no problema?
Ver solução completaUm carro de massa está fazendo uma curva circular de raio , que possui inclinação com o chão. Seja o coeficiente de atrito cinético e a magnitude da aceleração da gravidade. Derive uma expressão para um intervalo de velocidade possível necessário para manter o carro movendo no círculo sem derrapar. Expresse suas respostas através das constantes mencionadas no exercício.
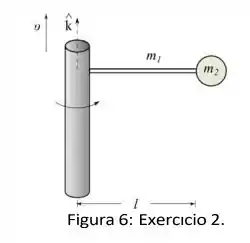
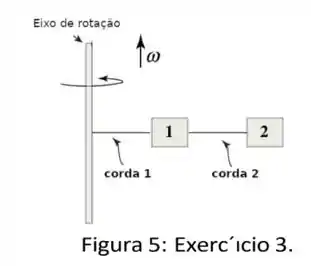
Ver solução completaDuas caixas e com massas e , respectivamente, estão presas por cordas a uma haste que gira com velocidade angular de magnitude . A caixa está a uma distância da haste e a caixa está a uma distância . Ignore as massas das cordas e o efeito da gravidade. Expresse suas respostas nas constantes descritas.
- Calcule , a tensão na corda que conecta a caixa na .
- Calcule , a tensão na corda que conecta a caixa na haste.
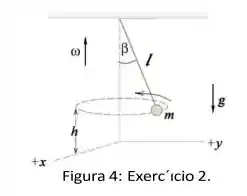
Uma bolinha de massa é suspensa por um cordão de comprimento , O cordão faz um ângulo com a vertical. A bolinha orbita em círculos com velocidade angular desconhecida, O plano orbital da bolinha está a uma altura do chão. Seja a constante da aceleração da gravidade, Ignore a resistência do ar.
- Descubra a velocidade angular . Use as constantes explicitadas no problema.
- A bolinha se solda do cordão e atinge o chão a uma distância horizontal de onde se soltou. Qual é essa distância ?
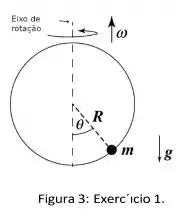
Uma bolinha está sobre um aro circular de raio que roda em torno do diâmetro com velocidade . Não há atrito.
- Qual deve ser a velocidade que mantém a bolina na mesma posição do aro, um ângulo com respeito a vertical?
- Analise a resposta anterior: Haverá um intervalos de velocidades angulares , para uma ângulo fixo . Descubra o valor de .
Adote as constantes citadas no exercício em suas respostas e como a magnitude da constante da aceleração da gravidade.
Ver solução completaUma moeda de massa está sobre um disco rígido a uma distância do centro do disco. Existe atrito entre a moeda e o disco e o coeficiente estático é . Num tempo , o disco começa a girar com uma aceleração angular constante de magnitude em torno do seu eixo central. A magnitude da aceleração da gravidade é . Expresse suas respostas em termos de , , , , e , se necessário.
- Qual é a magnitude máxima da força de atrito estático?
- Como a força de atrito estático varia em função do tempo?
- Qual a magnitude da velocidade angular que a moeda começa a deslizar do disco?
Dois satélites estão orbitando a Terra em altitudes diferentes. Assuma que as órbitas são circulares e os satélites têm a mesma massa. Qual satélite possui maior velocidade linear em torno da Terra? Qual satélite tem um maior período ?
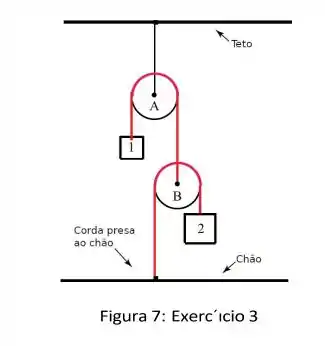
Ver solução completaDois blocos de massa e , estão presos num sistema de cordas e polias de massa desprezíveis. Calcule a aceleração do bloco , em termos das constantes do problema e da magnitude da aceleração da gravidade .
No final de uma corda de massa e comprimento está presa uma haste que gira com magnitude da velocidade angular . Na outra extremidade, está presa um objeto pontual de massa . Descubra a tensão na corda em função da distância da haste.
Assuma que o raio da haste é muito menor que o comprimento da corda. Ignore os efeitos da gravidade e expresse sua resposta em termo das variáveis e constantes apresentadas no problema.