UFSCAR, Sem Campus, Física 1, Listas Física 1 - UFSCAR - Lista 2 - Dinâmica, Questão 7
Uma moeda de massa está sobre um disco rígido a uma distância do centro do disco. Existe atrito entre a moeda e o disco e o coeficiente estático é . Num tempo , o disco começa a girar com uma aceleração angular constante de magnitude em torno do seu eixo central. A magnitude da aceleração da gravidade é . Expresse suas respostas em termos de , , , , e , se necessário.
- Qual é a magnitude máxima da força de atrito estático?
- Como a força de atrito estático varia em função do tempo?
- Qual a magnitude da velocidade angular que a moeda começa a deslizar do disco?
Passo 1
Eaew, tudo bem com você?
Temos aqui uma moedinha (ou qualquer coisa sem dimensão de massa ) a uma distância do centro de um disco. O atrito estático entre a moeda e a superfície do disco está relacionado a um coeficiente de atrito . Esse disco começa a girar com uma aceleração angular , e portanto, existe uma tendência da moeda ser jogada para fora (assim como a roupa é jogada para as paredes de uma máquina de lavar durante a centrifugação), no entanto, o atrito estático irá manter ela estacionária enquanto a tendência ao movimento não for grande o suficiente (ou seja, a velocidade angular não chegou à um valor que irá lançar a moeda para fora do disco). O esquema do exercício é o seguinte
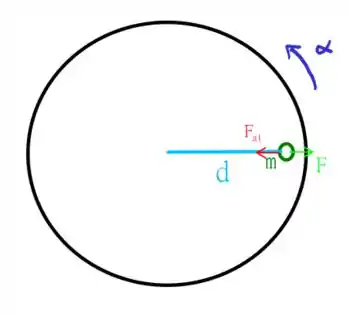
em que é uma força fictícia que representa a tendência da moeda ser jogada para fora! Vamos usar essas informações para resolver nosso problema! Saca só!
Passo 2
Primeiro vamos lembrar que a força de atrito estática tem por definição o valor máximo dado por
em que é a força normal, como temos que na vertical o equilíbrio é mantido, a força normal é igual ao peso da moeda, portanto
O primeiro item da questão é esse! O segundo é bastante direto, note que enquanto a moeda não ser arremessada, a força de atrito age como uma força centrípeta, e portanto, temos que
em que , e é o raio do movimento circular, temos então que
Mas quem é a velocidade angular neste caso? Consegue se lembrar?
Passo 3
Como temos uma aceleração angular constante e inicialmente o disco está parado, temos que a velocidade angular pode ser obtida através de um análogo da cinemática linear para o movimento circular
e, portanto, a nossa força de atrito estático evolui no tempo quadraticamente pela relação
Vamos usar isso para saber com qual velocidade angular a moeda é arremessada! Saca só!
Passo 4
Note que a força de atrito estático tem um valor máximo, e é essa força de atrito que mantém ela parada no lugar, se a velocidade angular aumentar o suficiente para atingir este valor, a moeda começará a se mover, portanto, vamos usar a igualdade
Isolando a velocidade angular, temos que
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
, e