UFSCAR, Sem Campus, Física 1, Listas Física 1 - UFSCAR - Lista 2 - Dinâmica, Questão 5
Duas caixas e com massas e , respectivamente, estão presas por cordas a uma haste que gira com velocidade angular de magnitude . A caixa está a uma distância da haste e a caixa está a uma distância . Ignore as massas das cordas e o efeito da gravidade. Expresse suas respostas nas constantes descritas.
- Calcule , a tensão na corda que conecta a caixa na .
- Calcule , a tensão na corda que conecta a caixa na haste.
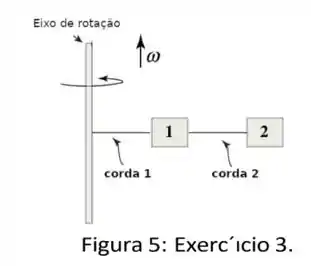
Passo 1
Eaew, tudo bem com você?
Primeiro, vou indicar aqui as tensões que são mencionadas no esquema, elas são as seguintes
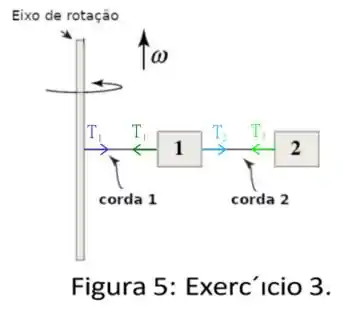
as cordas descritas no enunciado são inextensíveis, e estamos desconsiderando os efeitos da gravidade, portanto, tudo que precisamos nos preocupar é com o movimento circular de velocidade gerado pela rotação da haste. Mas como as caixas percebem isso? Elas estão se movendo em um movimento circular uniforme devido a presença de uma força centrípeta! Quem são essas forças para cada uma delas?
São as próprias tensões! Então vamos usar a velocidade angular e definições de aceleração centrípeta para encontrar as nossas tensões! Bora lá!
Passo 2
Na caixa temos duas forças atuando, então, pela segunda lei de Newton, temos que
em que é a aceleração centrípeta dada por
em que é o raio da circunferência delimitada pelo movimento circular, para a primeira caixa temos que , podemos relacionar a velocidade linear com a velocidade angular usando que , portanto, temos que
Analogamente, notando que para a caixa , temos apenas uma força atuando e que ela está a uma distância da haste, podemos escrever que
As equações e são o suficiente para resolvermos todo o problema! Bora terminar isso!
Passo 3
A tensão é dada diretamente pela equação , e usando ela na equação , temos que
e, portanto, temos que
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
e