UFSCAR, Sem Campus, Física 1, Listas Física 1 - UFSCAR - Lista 2 - Dinâmica, Questão 2
Uma bolinha está sobre um aro circular de raio que roda em torno do diâmetro com velocidade . Não há atrito.
- Qual deve ser a velocidade que mantém a bolina na mesma posição do aro, um ângulo com respeito a vertical?
- Analise a resposta anterior: Haverá um intervalos de velocidades angulares , para uma ângulo fixo . Descubra o valor de .
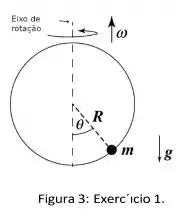
Adote as constantes citadas no exercício em suas respostas e como a magnitude da constante da aceleração da gravidade.
Passo 1
Eaew, tudo certinho contigo?
O enunciado não faz o melhor trabalho em deixar claro como funciona este movimento, mas a figura ajuda um pouco, temos o seguinte esquema
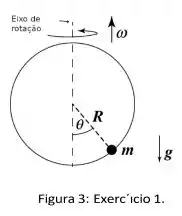
Note que o aro gira como uma moeda (Como fazemos quando estamos entediados e com uma moeda na mão!). Ao girar este aro, devido a velocidade angular , a bolinha fica estacionária em uma altura indicada pelo ângulo . Mas por quê?
Essa é uma posição de equilíbrio em que a força centrípeta que gera o movimento circular da bolinha (NÃO É AO LONGO DO ARO) é dada pela componente horizontal da força normal devido ao contato da bolinha no aro! Vamos usar esta condição de equilíbrio para encontrar a nossa velocidade! Vem comigo!
Passo 2
As forças são tais que
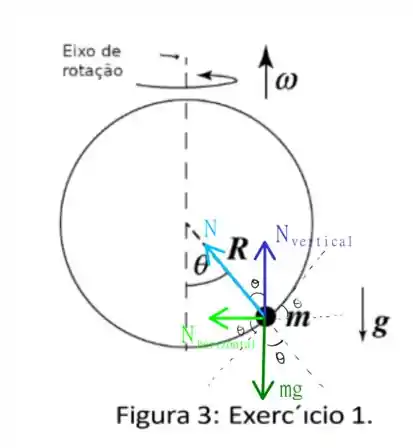
Vendo o seguinte esquema podemos usar a segunda lei de Newton para encontrar duas equações relevantes. Primeiro, temos a seguinte relação que será útil no futuro
e, como podemos identificar a componente horizontal como uma força centrípeta, temos que
Vamos usar essas duas equações para encontrar a nossa velocidade angular relacionada! Saca só!
Passo 3
Primeiro, podemos usar que
em que é a velocidade tangencial ao círculo que a bolinha faz ao girar em torno do eixo vertical. Essa velocidade é relacionada a velocidade angular através de , portanto, temos que
Note que é um raio, mas não o raio do aro, vamos encontrar quanto vale este raio daqui a pouquinho! Observando o esquema que temos montado no passo anterior, podemos verificar que
Portanto, usando a relação acima, obtemos que
ou, isolando , temos que
Mas ainda não sabemos quem é ! Vamos achar isso primeiro!
Passo 4
Da equa�o que montamos anteriormente, temos que
do esquema, no entanto, obtemos que , o que nos permite escrever
Isolando , temos que
de forma que a nossa velocidade angular é tal que
Vamos achar rapidamente quem é ! Bora lá!
Passo 5
Note que é a projeção de no plano em que o movimento circular acontece, como no seguinte esquema
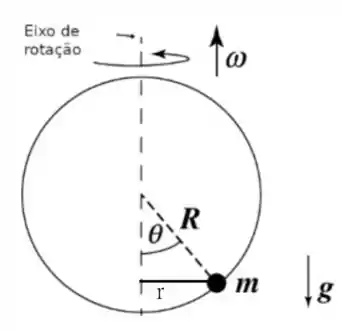
portanto, podemos usar que , e sendo assim, finalmente, a nossa velocidade angular é
Beleza! A primeira parte da questão foi isso! Vamos para a próxima!
Passo 6
Se o ângulo agora é fixo , temos que a velocidade angular toma a forma
mas note que nestas condições não existe realmente uma velocidade angular da bolinha. Pensa comigo, a bolinha é só um ponto no aro, agora com esta bolinha está na base do aro e portanto, nunca saí do lugar, nunca terá uma velocidade angular. O problema da relação acima pode ser mostrado se considerar que . Ou seja, a equação acima não tem validade, já que durante algumas passagens, nós dividimos por . É impossível determinar o intervalo dito nas condições apresentadas.
A questão foi isso! Te vejo na próxima!