UFSCAR, Sem Campus, Física 1, Listas Física 1 - UFSCAR - Lista 2 - Dinâmica, Questão 1
Uma ou duas forças agem sobre um disco metálico que se move sobre o gelo sem atrito ao longo do eixo , em movimento unidimensional. A massa do disco é . As forças , para direita, e , para esquerda, atuam ao longo do eixo e tem módulos e . Uma força faz um ângulo de com o eixo e tem módulo . Qual é a aceleração do disco quando apenas a força atua? Quando as forças e agem? E com todas as forças atuando sobre o disco?
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu um disco metálico que tá se movendo sem atrito ao longo do eixo , e que tem forças agindo sobre ele, mais ou menos assim:
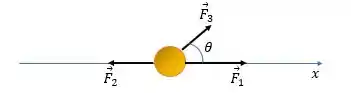
Ele diz que esse disco tem massa e as forças têm módulo:
A terceira força faz um ângulo com o eixo , então temos:
Beleza? Aí ele pede pra gente calcular a aceleração em três casos:
- quando só a força atua no disco
- quando e atuam no disco
- e quando , e .
E como é que a gente calcula essa aceleração? A gente vai considerar em cada caso, a força resultando que tá agindo no disco e calcular a aceleração usando a segunda lei de Newton:
Então, vamos lá!
Passo 2
Galera, vamos começar calculando a aceleração quando apenas a força atua no disco. Considerando o sentido do eixo positivo, e usando a equação:
Temos para e :
Passo 3
Agora vamos considerar que e atuam no disco:
Então, o somatório de forças nos dá:
Repare que tá no sentido contrário do eixo e por isso é negativo. Então, nós calculamos a aceleração fazendo:
Substituindo os valores, temos:
Passo 4
e quando , e agem no disco? Então nós temos:
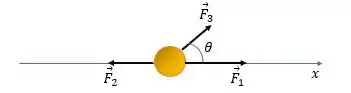
E aí a gente tem que somar todas as forças considerando sua direção novamente. Como faz um ângulo de com a horizontal, temos:
Substituindo os valores:
Isolando :
Logo, nossa aceleração é: