UFSCAR, Sem Campus, Física 1, Listas Física 1 - UFSCAR - Lista 2 - Dinâmica, Questão 9
No final de uma corda de massa e comprimento está presa uma haste que gira com magnitude da velocidade angular . Na outra extremidade, está presa um objeto pontual de massa . Descubra a tensão na corda em função da distância da haste.
Assuma que o raio da haste é muito menor que o comprimento da corda. Ignore os efeitos da gravidade e expresse sua resposta em termo das variáveis e constantes apresentadas no problema.
Passo 1
Eaew, tudo bem?
Aqui temos uma corda de massa (podemos pensar nela como uma segunda haste já que iremos desconsiderar os efeitos da gravidade). Na ponta dessa corda está presa uma massa que não tem dimensões, portanto, temos uma corda de massa que gira em torno de um eixo com velocidade com uma massa presa em sua ponta! Precisamos encontrar a tensão , em que é a distância do eixo de rotação para um ponto qualquer na corda! Parece um pouco complicado, não é?
Vamos tentar construir a expressão para a tensão avaliando a sua evolução ao longo da corda, lembrando do fato que a corda é uniforme, então a tensão ao longo de seu corpo está sempre relacionado a massas parciais que somam à massa total ! Saca só!
Passo 2
Em uma distância qualquer da haste sobre a corda, temos uma tensão , como no esquema a seguir
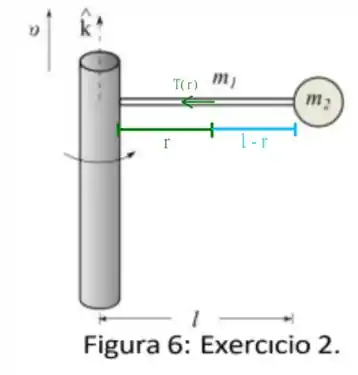
em toda posição que escolhemos, teremos que a tensão será responsável pela aceleração centrípeta naquela posição, no entanto, ainda temos um corpo rígido na ponta. Como o movimento de um corpo rígido se dá sobre o centro de massa, vamos considerar que a segunda parte da barra é um corpo de massa na posição do centro de massa da segunda parte, dada por
e, portanto, temos que a tensão será relacionada a seguinte expressão
Agora, precisamos analisar para descobrir quem é ! Vamos lá!
Passo 3
Como temos que a corda é uniforme, a razão de quantidade de massa por comprimento é a mesma em qualquer pedacinho dela, portanto, podemos escrever que
ou seja, isolando , obtemos
e a nossa tensão toma a forma
Essa é a expressão para a nossa tensão! Note que quando estivermos em , teremos o movimento circular de um corpo de massa , como seria esperado! Mas a tensão tem valores diferentes ao longo da corda! A questão foi isso! Te vejo na próxima! Tchau Tchau!