UFSCAR, Sem Campus, Física 1, Listas Física 1 - UFSCAR - Lista 2 - Dinâmica, Questão 4
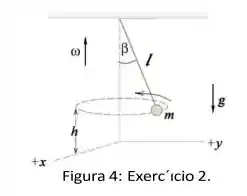
Uma bolinha de massa é suspensa por um cordão de comprimento , O cordão faz um ângulo com a vertical. A bolinha orbita em círculos com velocidade angular desconhecida, O plano orbital da bolinha está a uma altura do chão. Seja a constante da aceleração da gravidade, Ignore a resistência do ar.
- Descubra a velocidade angular . Use as constantes explicitadas no problema.
- A bolinha se solda do cordão e atinge o chão a uma distância horizontal de onde se soltou. Qual é essa distância ?
Passo 1
Oiie, tudo bem?
Esses enunciados são sempre melhor explicitados quando colocamos um diagrama das forças que atuam sobre a nossa partícula. Vamos usar o esquema dado no enunciado para introduzir estas forças, temos que
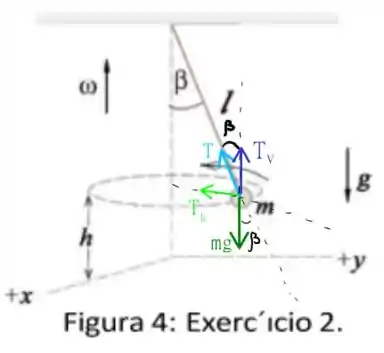
Temos que o movimento circular de velocidade angular é causado por uma força centrípeta, neste caso esta força é a componente horizontal da tensão do fio, . Essa informação é suficiente para encontrarmos a velocidade utilizando a segunda lei de Newton, e algumas relações conhecidas! Após a liberação da partícula, você pode imaginar como se o fio arrebentasse, a partícula se move como em um lançamento oblíquo com angulo inicial de lançamento , então analisando cinematicamente o movimento vertical e horizontal, seremos capazes de obter a distância . Vamos começar então!
Passo 2
Pela segunda lei de Newton, podemos escrever duas equações, uma para a dinâmica no que chamei de direção horizontal
em que é a aceleração centrípeta. E, uma para a direção vertical, no qual não há movimento, temos
Usando a definição de aceleração centrípeta, , na equação podemos escrever
em que é o raio da circunferência delimitada pelo movimento circular, e usei a definição , para relacionar a velocidade angular com a velocidade tangencial! Vamos trabalhar um pouco estas equações agora!
Passo 3
Temos que as componentes da tensão são obtidas observando o esquema como
e
da mesma forma, podemos obter o raio da circunferência como
desta maneira, a equação e , se tornam
e, também
ou simplificando, temos que
Ou seja, a nossa velocidade angular é dada por
Agora só precisamos achar quem é a nossa tensão! Vamos lá!
Passo 4
A tensão pode ser obtida diretamente da equação , temos que
e, portanto, a velocidade angular é dada por
tirando a raiz, temos que
Ótimo! A primeira parte da questão já foi! Vamos fazer agora a segunda!
Passo 5
Quando o fio arrebenta temos que a bolinha se solta com uma velocidade linear obtida usando que
usando que encontramos e como no esquema, temos que
Isso será a nossa velocidade inicial puramente horizontal! Enquanto, que a velocidade inicial vertical é zero! Mas qual a importância de sabermos isso? Após o fio se soltar temos que o movimento é dominado pelas duas equações cinemáticas, para a horizontal temos
em que , será obtido quando a bolinha percorrer um tempo , igual ao tempo que ela leva para cair! E como encontramos esse tempo? Através da equação que domina a vertical! Temos que
Vamos trabalhar estas equações! Vem comigo!
Passo 6
Primeiro, se queremos que a bolinha chegue ao chão, vamos considerar o instante de tempo em que , portanto, da equação , temos que
ou, isolando o tempo, temos
Maravilha! Se esse é o tempo que leva para a bolinha cair, podemos substituir na equação , junto com a equação como velocidade inicial, para obter a distância do ponto inicial , como
Apenas simplificando a expressão, temos que
Aí está! A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
e