UFSCAR, Sem Campus, Física 1, Listas Física 1 - UFSCAR - Lista 2 - Dinâmica, Questão 10
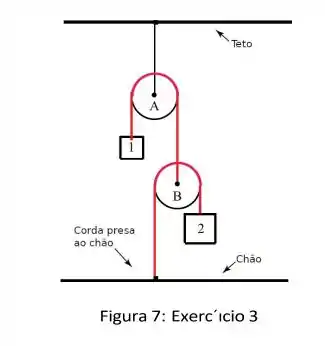
Dois blocos de massa e , estão presos num sistema de cordas e polias de massa desprezíveis. Calcule a aceleração do bloco , em termos das constantes do problema e da magnitude da aceleração da gravidade .
Passo 1
Eaew, tudo bem?
Aqui nós temos um sistema de polias móveis (elas tem que ser móveis, senão nada acontece neste problema), os blocos ligados as cordas tem massa e em que . Precisamos achar a aceleração sobre o bloquinho . O segredo para resolver isso é lembrar que as tensões em polias móveis se somam como o seguinte esquema
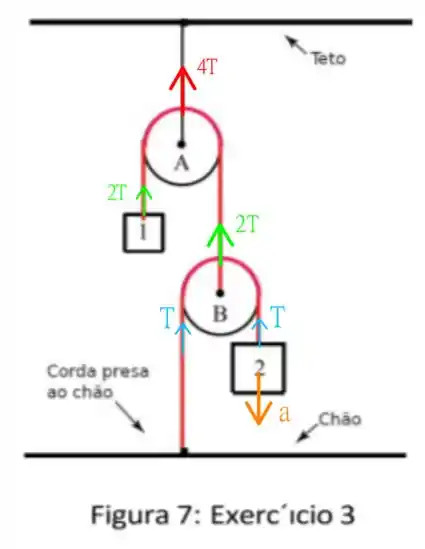
Note que estou propondo uma aceleração apontando para baixo no corpo , se esta escolha estiver errada, acharemos o resultado com sinal negativo! Vamos usar a segunda lei de Newton para montar as equações! Vem comigo!
Passo 2
A segunda lei de Newton para o corpo nos dá que
em que é o peso do corpo e a aceleração é dividida por devido a presença da polia móvel! Agora, para o segundo corpo, temos que
Usando estas duas equações seremos capazes de encontrar a nossa aceleração! Vamos lá!
Passo 3
Isolando a tensão na equação temos que
substituindo esta relação na equação temos que
Distribuindo o lado esquerdo para que possamos juntar os termos carregando a aceleração, temos que
Podemos passar os termos de aceleração para o mesmo lado para obter
Isolando então a aceleração, temos que
A questão é isso! Te vejo na próxima! Tchauzinho!