P1 de Física 1 da USP - 2013

Os satélites geoestacionários são aqueles que se encontram “parados” em relação a um ponto fixo na superfície terrestre (em geral, sobre a linha do equador terrestre). Por isso são usados como satélites de comunicação. Considere um satélite geoestacionário de massa com órbita circular de raio concêntrica com o globo terrestre. Adotando um sistema de referencial polar com centro no planeta Terra, determinar:

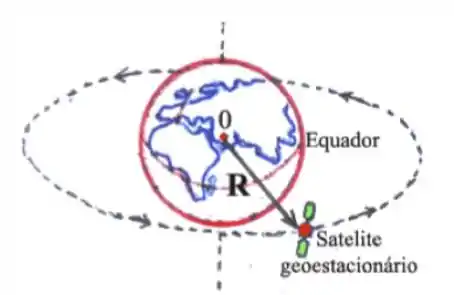
O período do movimento circular do satélite em segundos.

O raio da órbita circular em função do período do MCU (movimento circular uniforme), da massa da Terra, e da constante da gravitação universal, .

A velocidade escalar (ou módulo do vetor velocidade) em termos dos mesmos parâmetros da parte .

Um projétil é lançado por um canhão para atingir um alvo a uma distância , situada à mesma altura, com velocidade inicial . Um míssil balístico defensivo é lançado a partir do alvo, também a velocidade , quando o projétil atinge a sua altura máxima. Despreze a resistência do ar e considere a aceleração da gravidade como . Considere o míssil também em queda livre e tome o instante quando o míssil é lançado.

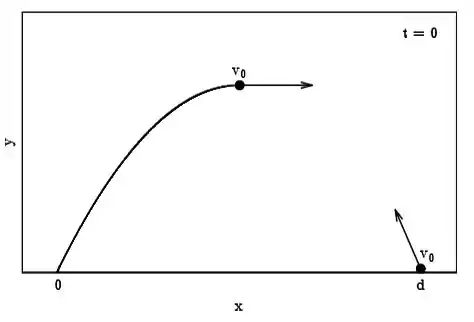
Calcule a altura máxima atingida pelo projétil.

Supondo que o ângulo de lançamento do míssil defensivo é suplementar ao de lançamento do projétil, determine esse ângulo em termos das quantidades dadas no enunciado.

Um elétron de massa e velocidade horizontal incide em uma região entre duas placas paralelas eletricamente carregadas, conforme mostra a figura abaixo. Ao percorrer essa região o elétron é submetido a uma forca vertical , constante, para cima. Sabendo-se que o comprimento das placas é igual a e desprezando o efeito da aceleração da gravidade, determine:

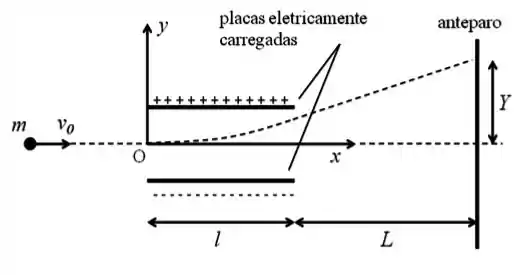
O vetor posição do elétron em função do tempo, quando este se encontra entre as placas paralelas eletricamente carregadas. Considere que a origem do sistema de coordenadas é do lado esquerdo das placas e que o elétron passa pela origem do sistema de coordenadas no instante , conforme mostra a figura. Expresse o resultado em termos de , , , e .

O valor de , quando o elétron atinge um anteparo situado a uma distancia das placas paralelas. Expresse o resultado em termos de , , , , .

Sabendo-se que a posição de uma partícula, em relação à origem do plano , é determinada pelo vetor:

Com em metros () e em segundos (), determine:

O vetor velocidade instantânea e o vetor aceleração instantânea em função do tempo.

O vetor velocidade instantânea no ponto e o vetor aceleração instantânea no ponto , ambos os pontos estão indicados no gráfico abaixo. Neste gráfico, a curva contínua representa a trajetória da partícula, descrita através do vetor posição

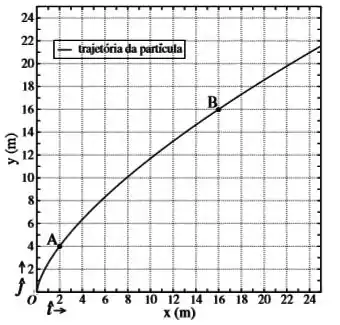
O vetor velocidade média e o vetor aceleração média , ambos entre os pontos e .