Um projétil é lançado por um canhão para atingir um alvo a uma distância , situada à mesma altura, com velocidade inicial . Um míssil balístico defensivo é lançado a partir do alvo, também a velocidade , quando o projétil atinge a sua altura máxima. Despreze a resistência do ar e considere a aceleração da gravidade como . Considere o míssil também em queda livre e tome o instante quando o míssil é lançado.

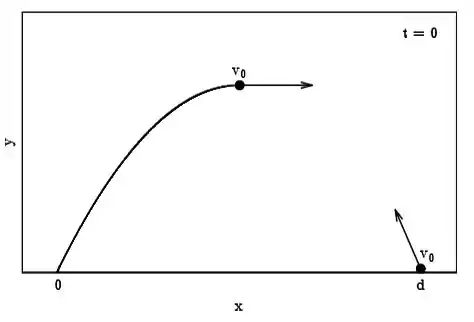
Calcule a altura máxima atingida pelo projétil.

Supondo que o ângulo de lançamento do míssil defensivo é suplementar ao de lançamento do projétil, determine esse ângulo em termos das quantidades dadas no enunciado.

Vamos desenhar a situação descrita:

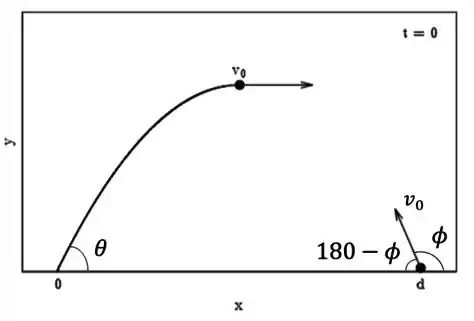
O problema nos informa que é suplementar à , ou seja, a soma dos dois é igual a radianos:

Decompondo nos eixos e , temos:

Sabemos que o alcance do projétil tem que ser , ele pode ser dado por:

Onde é o tempo que o projétil leva para retornar ao solo, esse tempo pode ser calculado por:

Onde

Isolando o :

Temos que:

Substituindo na expressão que encontramos anteriormente:

Que pode ser escrita como:

Lembrando-se da relação de duplicação de arcos:

Substituindo:

Logo, como

Temos: