Um elétron de massa e velocidade horizontal incide em uma região entre duas placas paralelas eletricamente carregadas, conforme mostra a figura abaixo. Ao percorrer essa região o elétron é submetido a uma forca vertical , constante, para cima. Sabendo-se que o comprimento das placas é igual a e desprezando o efeito da aceleração da gravidade, determine:

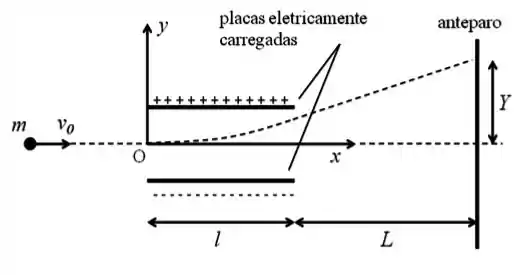
O vetor posição do elétron em função do tempo, quando este se encontra entre as placas paralelas eletricamente carregadas. Considere que a origem do sistema de coordenadas é do lado esquerdo das placas e que o elétron passa pela origem do sistema de coordenadas no instante , conforme mostra a figura. Expresse o resultado em termos de , , , e .

O valor de , quando o elétron atinge um anteparo situado a uma distancia das placas paralelas. Expresse o resultado em termos de , , , , .

Primeiramente precisamos saber quando que a força vai parar de atuar, que é no final da distância das placas que pode ser calculada com a expressão do item anterior.

Logo, neste instante a equação da posição muda, por que agora o eixo não terá mais a força atuando e portanto também não terá mais aceleração, passando a ser um movimento MRU dado por:

Onde é a posição quando e é a componente da velocidade neste mesmo instante . Vamos calcular isso.

O vetor velocidade pode ser calculado por:

Logo:

Logo:

Muito bem, agora para achar :

Temos então que:

Substituindo o valor de :

Portanto nosso novo é:

O projétil irá atingir o anteparo no instante:

Portanto: