Os satélites geoestacionários são aqueles que se encontram “parados” em relação a um ponto fixo na superfície terrestre (em geral, sobre a linha do equador terrestre). Por isso são usados como satélites de comunicação. Considere um satélite geoestacionário de massa com órbita circular de raio concêntrica com o globo terrestre. Adotando um sistema de referencial polar com centro no planeta Terra, determinar:
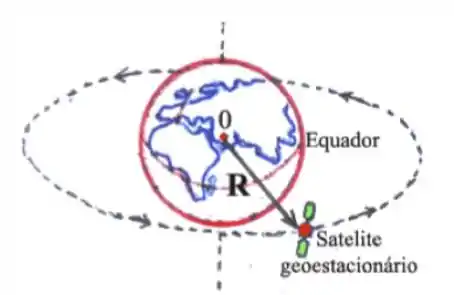
O período do movimento circular do satélite em segundos.
O raio da órbita circular em função do período do MCU (movimento circular uniforme), da massa da Terra, e da constante da gravitação universal, .
A velocidade escalar (ou módulo do vetor velocidade) em termos dos mesmos parâmetros da parte .
Passo 1
Para que um satélite seja geoestacionário sua velocidade angular () tem que ser igual à velocidade angular associada ao deslocamento de um ponto no equador terrestre:
Para isso, basta que os períodos sejam iguais. Tendo em vista que o período de rotação da terra é de 24 horas, temos:
Passo 2
A força centrípeta agindo sobre o satélite é a força de atração gravitacional entre o satélite e a Terra. Podemos escrever:
A partir da lei de Newton podemos escrever:
Isolando o , temos:
Entretanto o enunciado não quer que apareça na expressão, ele quer que apareça o período .
Lembramos que
E também que:
Substituindo:
Assim, em termos do período, a distancia até o centro da terra obedece a relação:
Passo 3
Do item anteriores temos que:
Substituindo o encontrado no item anterior:
Jogando o e o para dentro da raiz cubica: