Sabendo-se que a posição de uma partícula, em relação à origem do plano , é determinada pelo vetor:
Com em metros () e em segundos (), determine:
O vetor velocidade instantânea e o vetor aceleração instantânea em função do tempo.
O vetor velocidade instantânea no ponto e o vetor aceleração instantânea no ponto , ambos os pontos estão indicados no gráfico abaixo. Neste gráfico, a curva contínua representa a trajetória da partícula, descrita através do vetor posição
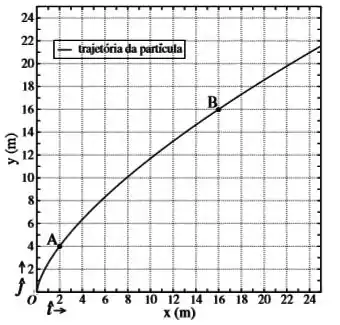
O vetor velocidade média e o vetor aceleração média , ambos entre os pontos e .
Passo 1
Lembrando que o vetor velocidade nada mais é do que a derivada do vetor posição, portanto:
E por sua vez, a aceleração é a derivada da velocidade, então:
Passo 2
Já possuímos as equações do vetor velocidade e aceleração, mas ambos estão em função do tempo. Então para utilizá-los precisamos do instante de tempo do ponto e do ponto . Para descobrir o tempo, basta substituir as coordenadas do ponto na equação da posição.
Igualando as componentes de e :
Ou
Logo, o ponto corresponde ao instante .
Fazemos o mesmo para o ponto .
Igualando as componentes de e :
Ou
Logo o ponto B corresponde ao instante .
Agora substituindo, temos que a velocidade instantânea no ponto é:
E agora o vetor aceleração instantânea no ponto
Passo 3
Bem, nós calcularemos a velocidade média com a fórmula:
E a aceleração média com a fórmula:
Observando ambas as fórmulas vemos que ainda nos falta calcular , e que são respectivamente, , e . Então, mãos a obra:
Show! Agora já temos tudo para calcular as médias.
Velocidade média.
Aceleração média.