P3 de Física 1 da USP - 2012

Uma partícula de massa e velocidade desliza sobre uma superfície horizontal e colide com um quadrado formado por barras rígidas de massa desprezível e comprimento , que possui partículas de massa em três dos seus vértices, como mostrado na figura (vista de cima). O quadrado está inicialmente em repouso, e o atrito entre todos os corpos e a superfície pode ser desprezado. Após a colisão, a partícula fica colada ao quadrado no vértice que estava vazio. Expresse todas as respostas em função de , e .

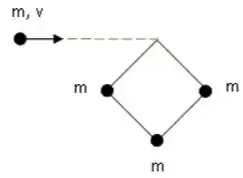
(a) Que grandezas físicas relevantes para o problema são conservadas na colisão? Justifique sua resposta.

(b) Determine o momento de inércia do sistema, após a colisão, em torno do eixo de rotação relevante para o problema.

(c) Determine o vetor velocidade de translação do centro de massa do sistema após a colisão.

(d) Determine o vetor velocidade angular de rotação do sistema em torno do seu eixo.

(e) Qual é a variação de energia cinética do sistema devido à colisão?

Um alvo é constituído por uma placa quadrada de lado e massa que pode girar sem atrito em volta de um eixo passando por um dos seus lados. O eixo é fixado horizontalmente numa parede e o alvo colocado na sua posição de repouso, conforme mostrado na figura. Em seguida, ele é atingido frontalmente em seu centro por uma partícula de massa e velocidade que fica retida no centro da placa. Usando o ponto como origem quando for preciso, e supondo ( vezes a massa da partícula), responda às seguintes perguntas, expressando suas respostas em termos de , , e .

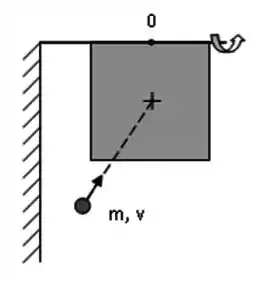
(a) Calcule o momento de inércia total do sistema depois da colisão em torno do seu eixo de rotação, sabendo que o momento de inércia de uma barra delgada de mesma massa e largura em relação a um eixo passando pelo seu centro (e perpendicular à barra) é .

(b) Qual é a velocidade angular da placa logo após o impacto da bala?

(c) Qual é a altura máxima atingida pelo centro de massa da placa antes que ela comece a oscilar em torno da sua posição vertical inferior?

(d) Qual é a aceleração angular da placa, naquela altura máxima, expressada em função do ângulo que ela faz em relação à sua posição de repouso?

A hélice propulsora de um avião possui comprimento (de uma extremidade a outra) e massa . Logo no início do funcionamento do motor, ele aplica um torque de na hélice, que começa a se mover a partir do repouso. O momento de inércia da hélice em relação ao eixo perpendicular ao plano da hélice passando pelo seu centro de massa é .

(a) Construir o gráfico do ângulo de rotação em função do tempo , considerando a unidade de em revoluções e do tempo em segundos (). Também construa o gráfico da velocidade angular em função do tempo (). Considere na construção de ambos os gráficos os instantes e .

(b) Qual é o trabalho realizado pelo motor durante as . iniciais? Utilize a unidade do trabalho realizado em Joule .

(c) Qual é a potência média fornecida pelo motor durante as iniciais? Utilize a unidade da potência em Watts .

(d) Qual é a potência instantânea do motor no instante em que a hélice propulsora completa essas .? Utilize a unidade da potência em Watts .

Um cilindro homogêneo de massa e raio está em repouso sobre o topo de uma mesa. Um fio é ligado por meio de um suporte duplo preso às extremidades de um eixo sem atrito passando pelo centro do cilindro de modo que o cilindro pode girar em torno do eixo. O fio (inextensível e de massa desprezível) passa sobre uma polia em forma de disco de massa e raio montada em um eixo sem atrito que passa pelo seu centro. Um bloco de massa é suspenso na extremidade livre do fio. O fio não desliza sobre a polia e o cilindro rola sem deslizar sobre o topo da mesa. O sistema é liberado a partir do repouso.

Expresse seus resultados em termos dos dados do problema ( e ) e da aceleração da gravidade .

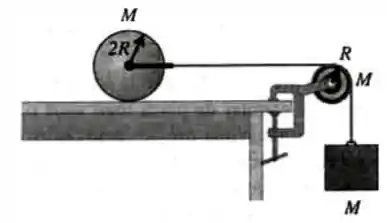
(a) Esboce diagramas de corpo livre (indicando as forças atuantes) do cilindro, da polia e do bloco.

(b) Calcule a aceleração do bloco.

(c) Determine o módulo do torque resultante na polia.

(d) Calcule o coeficiente de atrito estático entre o cilindro e a mesa.

Dados: polia de massa e raio , eixo perpendicular ao plano do disco passando pelo centro: . Cilindro de massa e raio , eixo central .