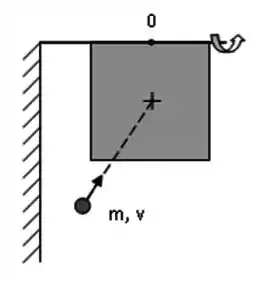
Um alvo é constituído por uma placa quadrada de lado e massa que pode girar sem atrito em volta de um eixo passando por um dos seus lados. O eixo é fixado horizontalmente numa parede e o alvo colocado na sua posição de repouso, conforme mostrado na figura. Em seguida, ele é atingido frontalmente em seu centro por uma partícula de massa e velocidade que fica retida no centro da placa. Usando o ponto como origem quando for preciso, e supondo ( vezes a massa da partícula), responda às seguintes perguntas, expressando suas respostas em termos de , , e .
(a) Calcule o momento de inércia total do sistema depois da colisão em torno do seu eixo de rotação, sabendo que o momento de inércia de uma barra delgada de mesma massa e largura em relação a um eixo passando pelo seu centro (e perpendicular à barra) é .
(b) Qual é a velocidade angular da placa logo após o impacto da bala?
(c) Qual é a altura máxima atingida pelo centro de massa da placa antes que ela comece a oscilar em torno da sua posição vertical inferior?
(d) Qual é a aceleração angular da placa, naquela altura máxima, expressada em função do ângulo que ela faz em relação à sua posição de repouso?
Passo 1
(a)
Pelo teorema dos eixos paralelos:
Onde é a distância até o novo eixo, ou seja, a distância do centro de massa até o ponto , que é . Substituindo:
Como , então:
Perfeito. Entretanto, o sistema não é apenas composto pela placa, temos também a partícula que fica alojado na placa. Para calcular o momento de inércia de qualquer partícula vale a fórmula:
Onde é a distância até o eixo de rotação, que nesse caso, como a partícula atinge o centro da barra, a distância até o ponto , será . Substituindo:
Agora para obter o momento de inércia do sistema é só somar.
Passo 2
(b)
Como estamos trabalhando com um sistema isolado, sem forças externas, também não haverá torques externos. Ok, mas e dai? Bem, se a gente lembrar bem, tínhamos duas fórmulas que diziam:
Em outras palavras, sem força externa e torque externo, os momentos linear e angular se conservam.
Como estamos interessados em descobrir a velocidade angular, é interessante utilizar a conservação do momento angular antes e depois da colisão.
Vamos utilizar .
Como a distância da partícula até a placa era antes mesmo da colisão, em módulo vai ficar:
Agora para calcular o momento angular final, vamos utilizar a fórmula , pois o nosso interesse é em descobrir a velocidade angular.
Fazendo agora a conservação do momento angular:
Passo 3
(c)
Logo após a colisão, depois que a partícula fica retida na placa, a energia mecânica do sistema entre a posição inicial e a altura máxima se conserva. Assim, calculando a energia mecânica antes e depois:
Entretanto, estamos considerando a posição logo após a colisão como sendo a altura inicial zero. Portanto não temos energia potencial gravitacional. Além disso, o sistema está preso ao eixo de rotação, então ele não possui translação, apenas rotação. Logo a energia cinética é apenas de rotação. Ficamos então com:
Agora, no ponto mais alto que o sistema poderá atingir, a energia mecânica será dada por:
Entretanto, no ponto mais alto o sistema está em um momento de inversão de movimento, ou seja, ele chegou ao ponto mais alto, parou por um instante e começará a fazer o movimento no sentido contrário. Logo, no ponto mais alto ele terá velocidade nula, ou seja, não terá energia cinética! Apenas energia potencial. Ficamos então com:
Aplicando a conservação de energia mecânica:
Passo 4
(d)
Vamos fazer um desenho genérico da situação para entender melhor:
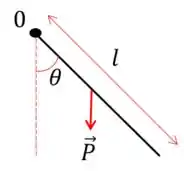
Para analisarmos o que está acontecendo, precisamos decompor a força peso em:
A componente está na direção do eixo e portanto não produzirá torque, entretanto a componente produzirá torque, que pode ser calculado por:
Onde é a distancia até o eixo de rotação que nada mais é que . Substituindo em módulo ficará:
Lembrando que .
Agora como o problema quer a aceleração angular, basta utilizar a fórmula:
Substituindo o torque que encontramos:
Resposta
a)
b)
c)
d)