A hélice propulsora de um avião possui comprimento (de uma extremidade a outra) e massa . Logo no início do funcionamento do motor, ele aplica um torque de na hélice, que começa a se mover a partir do repouso. O momento de inércia da hélice em relação ao eixo perpendicular ao plano da hélice passando pelo seu centro de massa é .
(a) Construir o gráfico do ângulo de rotação em função do tempo , considerando a unidade de em revoluções e do tempo em segundos (). Também construa o gráfico da velocidade angular em função do tempo (). Considere na construção de ambos os gráficos os instantes e .
(b) Qual é o trabalho realizado pelo motor durante as . iniciais? Utilize a unidade do trabalho realizado em Joule .
(c) Qual é a potência média fornecida pelo motor durante as iniciais? Utilize a unidade da potência em Watts .
(d) Qual é a potência instantânea do motor no instante em que a hélice propulsora completa essas .? Utilize a unidade da potência em Watts .
Passo 1
(a)
Muito bem, para construir esses gráficos vamos precisar das equações que governam essas quantidades.
Vamos começar pelo gráfico de :
Sabemos que o ângulo percorrido é dado pela equação:
Entretanto o problema nos informa que a hélice começa a se mover a partir do repouso. Portanto temo e . Restando apenas:
Que é a equação de uma parábola com vértice na origem.
Vamos encontrar agora a equação para o gráfico de :
Sabemos que a velocidade angular é dada pela equação:
Entretanto, como a hélice parte do repouso ficamos apenas com:
Que é a equação de uma reta que passa pela origem.
Agora já temos como é o formato do gráfico as equações de cada gráfico. Falta determinar o para podermos substituir nas equações e determinar os pontos em qualquer instante de tempo.
A segunda lei de Newton para a rotação nos dá que:
Logo:
Os valores do torque e do momento de inércia já foram dados no problema, basta substitui-los.
Muito bem, achamos a aceleração angular. Entretanto falta um detalhe importante. O gráfico é de revoluções, ou seja, voltas. Não é de radianos. Então precisamos converter, mas é bem fácil. Basta lembrar que 1 volta corresponde a radianos.
Logo, substituindo na equação dos gráficos temos:
:
Calculando os instantes pedidos no enunciado:
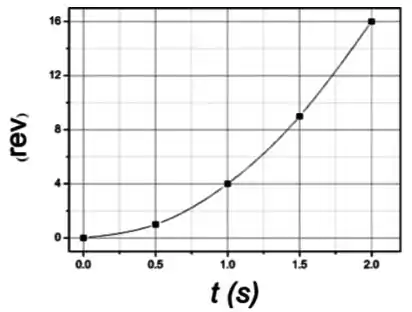
Agora o gráfico de :
Calculando nos instantes pedidos no problema:
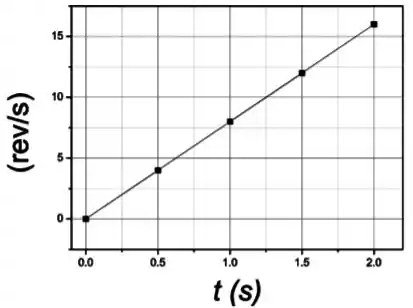
Passo 2
(b)
Lembra que trabalho é igual a força x deslocamento? Então, na rotação é a mesma coisa. O trabalho vai ser igual a força de rotação(torque) x deslocamento rotacional ( radianos):
O problema quer o trabalho nas 9 revoluções iniciais. Entretanto, tem um detalhe. Precisamos passar essas revoluções para radianos. É o mesmo macete, uma revolução tem , logo:
Substituindo:
Passo 3
(c)
Lembrando que a fórmula da potência média é dada por:
Já possuímos o trabalho realizado. Falta só encontrar quanto tempo leva para completar 9 revoluções. Vamos utilizar a fórmula que encontramos para o gráfico no item :
Substituindo:
Agora é só substituir tudo na fórmula da potência:
Passo 4
(d)
Para calcular a potência instantânea, basta colocar no formato diferencial:
Lembrando que:
Como o torque é constante, colocando na forma diferencial fica:
Substituindo na potencia instantânea:
No entanto, sabemos que:
Restando apenas:
Agora só falta calcular o valor de em usando a equação do item :
O tempo de 9 revoluções já encontramos no item anterior, .
Agora passando para radianos:
Substituindo agora na fórmula da potência instantânea:
Resposta
(a)
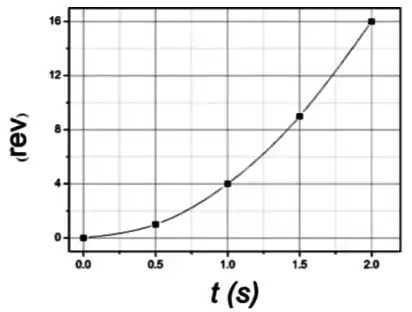
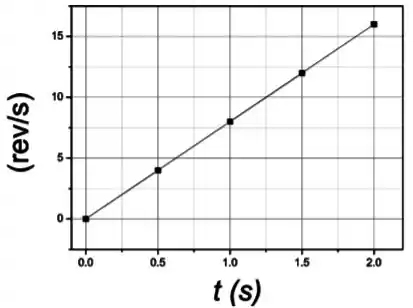
(b)
(c)
(d)