Uma partícula de massa e velocidade desliza sobre uma superfície horizontal e colide com um quadrado formado por barras rígidas de massa desprezível e comprimento , que possui partículas de massa em três dos seus vértices, como mostrado na figura (vista de cima). O quadrado está inicialmente em repouso, e o atrito entre todos os corpos e a superfície pode ser desprezado. Após a colisão, a partícula fica colada ao quadrado no vértice que estava vazio. Expresse todas as respostas em função de , e .
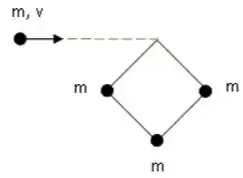
(a) Que grandezas físicas relevantes para o problema são conservadas na colisão? Justifique sua resposta.
(b) Determine o momento de inércia do sistema, após a colisão, em torno do eixo de rotação relevante para o problema.
(c) Determine o vetor velocidade de translação do centro de massa do sistema após a colisão.
(d) Determine o vetor velocidade angular de rotação do sistema em torno do seu eixo.
(e) Qual é a variação de energia cinética do sistema devido à colisão?
Passo 1
(a)
Sabemos que:
Ou seja, o momento linear só muda se houver a presença de forças externas ao sistema. Como não tem forças externas ao sistema, o momento linear é conservado!
Além disso, sabemos que:
Ou seja, o momento angular só muda se houver a presença de torque externo ao sistema. Como não tem forças externas ao sistema, também não terá torque externo ao sistema e o momento angular será conservado!
Como após a colisão a partícula fica colada ao sistema, a colisão é totalmente inelástica e a energia cinética não será conservada.
Passo 2
(b)
Sabemos que o momento de inércia para partículas pode ser calculado por:
E o momento de inércia total é a soma dos momentos de inércia das partículas. Mas como as 4 partículas tem a mesma massa e a mesma distância até o centro do quadrado, elas terão o mesmo momento de inércia! Logo, para achar o momento de inércia, basta multiplicar o momento de inércia de uma partícula por 4.
A distância até o centro do quadrado é a metade da diagonal, ou seja . Logo:
Passo 3
(c)
Fazendo a conservação do momento linear Teremos:
No momento inicial, as três partículas estão em repouso, apenas uma possui velocidade, então:
Passo 4
(d)
Já utilizamos a conservação do momento linear, só falta a conservação do momento angular, é ela mesma que vamos usar!
Onde é a distância até o eixo que é o centro do quadrado. Olhando direitinho dá para ver que essa distância é metade da diagonal do quadrado, ou seja, . Então:
Como o problema está querendo a velocidade angular, é interessante que utilizemos outra fórmula para o momento angular final, da forma que explicite a velocidade angular na nossa equação, lembra qual é?
O momento de inércia já foi calculado no item , basta substituir:
Como explicado no item , o momento angular é conservado. Então igualando o final e inicial:
Pronto! Já temos o módulo da velocidade angular, só falta agora a direção e sentido.
Para descobrir a direção e sentido, vamos olhar para o momento angular, pois:
Logo o momento angular tem que ter a mesma direção e sentido da velocidade angular.
Agora, olhando para a outra fórmula:
Conseguimos descobrir a direção e sentido pela regra da mão direita. Reescrevendo em termos dos vetores unitários ficará:
Pela regra da mão direita temos que:
Então ficamos com:
Ou seja, como a velocidade angular tem a mesma direção e sentido do momento angular, ela terá o sentido , ou seja, perpendicular ao quadrado e apontando para baixo.
Passo 5
(e)
Basta calcular a energia cinética final e inicial. A inicial é dada por:
Entretanto a energia cinética final é dada pela energia cinética de rotação e energia cinética de translação.
Substituindo o momento de inércia, a velocidade de centro de massa e a velocidade angular que encontramos nos itens anteriores:
Agora podemos calcular a variação da energia cinética:
Resposta
a) Momento angular e linear.
b)
c)
d)
e)