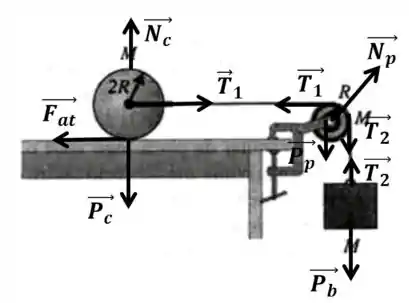
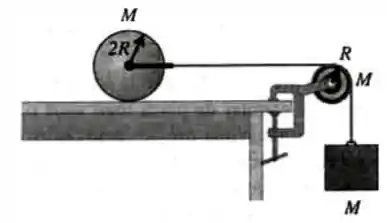
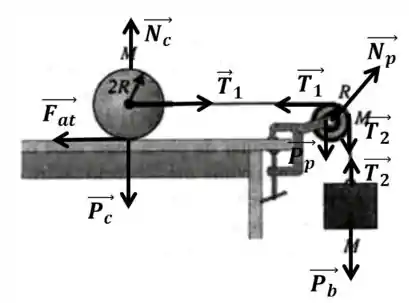
Um cilindro homogêneo de massa e raio está em repouso sobre o topo de uma mesa. Um fio é ligado por meio de um suporte duplo preso às extremidades de um eixo sem atrito passando pelo centro do cilindro de modo que o cilindro pode girar em torno do eixo. O fio (inextensível e de massa desprezível) passa sobre uma polia em forma de disco de massa e raio montada em um eixo sem atrito que passa pelo seu centro. Um bloco de massa é suspenso na extremidade livre do fio. O fio não desliza sobre a polia e o cilindro rola sem deslizar sobre o topo da mesa. O sistema é liberado a partir do repouso.
Expresse seus resultados em termos dos dados do problema ( e ) e da aceleração da gravidade .
(a) Esboce diagramas de corpo livre (indicando as forças atuantes) do cilindro, da polia e do bloco.
(b) Calcule a aceleração do bloco.
(c) Determine o módulo do torque resultante na polia.
(d) Calcule o coeficiente de atrito estático entre o cilindro e a mesa.
Dados: polia de massa e raio , eixo perpendicular ao plano do disco passando pelo centro: . Cilindro de massa e raio , eixo central .
Passo 1
(a)
Para desenhar esse diagrama temos que ficar atento que as trações nos dois lados da polia são diferentes! E que a direção da força normal na polia é contraria ao apoio que a sustenta que está na diagonal. Muito bem, ficando atento a isso. Montamos o seguinte diagrama:
Passo 2
(b)
Como todos os objetos estão conectados por uma corda de massa desprezível, a aceleração dos três será a mesma. Então vamos aplicar a lei de rotação e de translação .
Para o cilindro, temos:
Aplicando a lei de translação:
Aplicando a lei de rotação:
Lembrando que :
Como o cilindro rola sem deslizar, podemos utilizar a relação:
Então a segunda equação fica:
Substituindo na equação que encontramos para a translação teremos:
Para a polia, temos:
Aplicando a lei de rotação temos:
Lembrando que , e no caso da polia temos forças aplicando torque em sentidos contrários, então teremos:
Como a corda não desliza sobre a polia, podemos aplicar a relação:
Logo, substituindo:
Substituindo a equação que achamos para o cilindro temos:
E por fim, analisando o bloco, temos:
Aplicando a lei de translação temos:
Substituindo o valor de que achamos ao analisar a polia, temos:
Passo 3
(c)
Da equação da lei de rotação que usamos para a polia, temos que:
Substituindo temos:
Substituindo a aceleração que achamos no item anterior:
Passo 4
d)
Da equação que encontramos para o cilindro no item , temos que:
Como , temos:
A força de atrito é dada por:
Então o coeficiente de atrito estático será dado por:
Substituindo e