Listas de Estudos pra Prova - Tipler Vol 1 - 6°ed de Física 1 da UTFPR - Trabalho e Conservação de Energia

(Cap 6 – Ex 2) Você empurra uma caixa pesada sobre uma mesa horizontal com atrito, em linha reta. A caixa parte do repouso e acaba em repouso. Descreva o trabalho realizado sobre ela (incluindo sinais) por cada uma das forças que atuam sobre ela e diga qual é o trabalho resultante realizado.

(Cap 7 – Ex 15) Suponha que sua taxa metabólica máxima (a taxa máxima na qual seu corpo utiliza sua energia química) é de 1500 W (cerca de 2,7 hp). Supondo uma eficiência de 40 por cento para a conversão de energia química em energia mecânica, estime o seguinte: (a) o menor tempo que você levaria para subir quatro lances de escada, se cada lance tem a altura de 3,5 m, (b) o menor tempo que você levaria para subir o Empire State Building (102 andares) usando o resultado da Parte (a). Comente sobre a viabilidade de você atingir o resultado da Parte (b).

(Cap 6 – Ex 49) Uma força única de 5,0 N, com a orientação de +x, atua sobre um objeto de 8,0 kg. (a) Se o objeto parte do repouso em x = 0 no tempo t = 0, escreva uma expressão para a potência desenvolvida por esta força, como função do tempo. (b) Qual é a potência desenvolvida por esta força no tempo t = 3,0 s?

(Cap 6 – Ex 23) Encontre a energia cinética de (a) uma bola de beisebol de 0,145 kg movendo-se a uma velocidade de ; e (b) um corredor de 60,0 kg correndo a um ritmo constante de .

(Cap 6 – Ex 58) Um dos mais potentes guindastes do mundo está em operação na Suíça. Ele pode, lentamente, elevar uma carga de 6000 t até uma altura de 12,0 m (1 t = 1000 kh). (a) Qual é o trabalho realizado pelo guindaste durante esta tarefa? (b) Se 1 min é o tempo para levantar essa carga a essa altura, com velocidade constante, e o guindaste tem urna eficiência de 20 por cento, encontre a potência (bruta) total do guindaste.

(Cap 6 – Ex 24) Uma caixa de 6,0 kg é levantada de uma altura de 3,0 m, a partir do repouso, por uma força aplicada vertical de 80 N. Encontre (a) o trabalho realizado sobre a caixa pela força aplicada, (b) o trabalho realizado sobre a caixa pela gravidade e (c) a energia cinética final da caixa.

(Cap 6 – Ex 25) Uma força constante de 80 N atua sobre uma caixa de 5,0 kg. A caixa está, inicialmente, se movendo a 20 m/s no sentido da força e, 3,0 s depois, ela se move a 68 m/s. Determine o trabalho realizado por esta força e a potência média por ela desenvolvida durante o intervalo de 3,0 s.

(Cap 6 – Ex 65) Uma partícula de massa m se move ao longo do eixo x. Sua posição varia no tempo de acordo com , onde x estå em metros e t está em segundos. Determine (a) a velocidade e a aceleração da partícula como funções de t, (b) a potência fornecida à particula em função de t e (c) o trabalho realizado pela força resultante entre e .

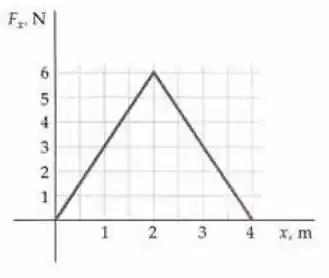
(Cap 6 – Ex 27) Uma partícula de 3,0 kg, que se move ao longo do eixo x, tem uma velocidade de +2,0 m/s quando passa pela origem. Ela está sujeita a uma força única, , que varia com a posição como mostrada na figura abaixo. (a) Qual é a energia cinética da partícula quando ela passa pela origem? (b) Qual é o trabalho realizado pela força, enquanto a partícula se move de x = 0,0 m até x = 4,0 m? (c) Qual é a rapidez da partícula quando ela está em x = 4,0 m?

(Cap 7 – Ex 65) O bloco de na figura desce por uma rampa curvada sem atrito, partindo do repouso a uma altura de . O bloco então desliza por sobre uma superfície horizontal rugosa até atingir o repouso. (a) Qual é a rapidez do bloco na base da rampa? (b) Qual é a energia dissipada por atrito? (c) Qual é o coeficiente de atrito cinético entre o bloco e a superfície horizontal?

(Cap 7 – Ex 39) O objeto de da Figura 7-42 é liberado do repouso a uma altura de em uma rampa curva sem atrito. Na base da rampa está uma mola com uma constante de força igual a . O objeto desliza rampa abaixo até a mola, comprimindo-a uma distância até atingir momentaneamente o repouso.

(a) Encontre .

(b) Descreva o movimento do objeto (se ocorrer) após o repouso momentâneo ?

(Cap 7 – Ex 25) A força é associada à função energia potencial , onde é uma constante positiva.

(a) Determine a força como função de .

(b) Essa força está apontando para a origem ou para longe dela, na região ? Repita a pergunta para a região.

(c) A energia potencial aumenta ou diminui quando cresce na região?

(d) Responda às Partes (b) e (c) com a constante negativa.

(Cap 7 – Ex 51a) Uma bola (de ) é lançada do teto de um edifício, acima do chão. Sua velocidade inicial é de , formando acima da horizontal. Despreze a resistência do ar.

a) Qual a altura máxima, acima do chão, atingida pela bola?

(Cap 7 – Ex 38) Um bloco de desliza ao longo de uma superfície horizontal sem atrito com uma velocidade de (Figura 7-41). Após deslizar por uma distância de , o bloco faz uma suave transição para uma rampa sem atrito inclinada a um ângulo de 40° com a horizontal. Qual a distância, ao longo da rampa, que o bloco percorre até atingir momentaneamente o repouso?

(Cap 7 – Ex 34) Uma máquina de Atwood, consiste em duas massas, e , e uma polia sem massa e sem atrito. Partindo do repouso, a rapidez das duas massas chega a ao final de . Nesse tempo, a energia cinética do sistemas atinge e cada massa terá se deslocado uma distância de . Determine os valores de e .

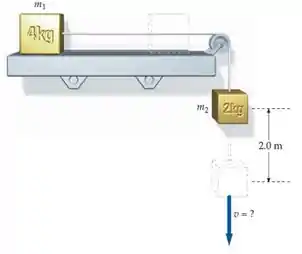
(Cap 7 – Ex 67) Na figura abaixo, o coeficiente de atrito cinético entre o bloco de e a prateleira é . (a) Encontre a energia dissipada por atrito quando o bloco de cai por uma distância . (b) Encontre a variação na energia mecânica do sistema dois-blocos-Terra durante o tempo que o bloco de leva para cair pela distância . (c) Use seu resultado da parte (b) para encontrar a rapidez de um dos blocos depois que o bloco de cai por .

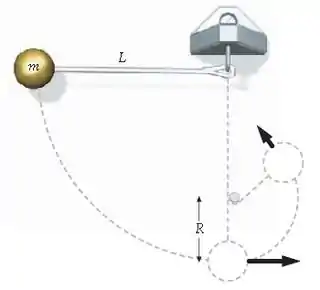
(Cap 7 – Ex 101) Um pêndulo consiste em uma pequena bola de massa presa a um fio de comprimento A bola é segurada lateralmente com o fio na horizontal (Figura 7-56). Então ela é largada do repouso. No ponto mais baixo da trajetória, o fio se prende a um pequeno prego, a uma distância acima desse ponto. Mostre que deve ser menor do que para que o fio permaneça tenso enquanto a bola completa uma volta inteira em torno do prego.

(Cap 7 – Ex 51b) Uma bola (de ) é lançada do teto de um edifício, acima do chão. Sua velocidade inicial é de , formando acima da horizontal. Despreze a resistência do ar.

b) Qual é a rapidez da bola ao chegar no chão