Listas de Estudos pra Prova - Halliday Vol 1 - 8°ed de Física 1 da UTFPR - Energia Potencial e Conservação da Energia

(Capítulo 8.5 – Exercício 16)

(a) No Problema 7, qual é a velocidade da bola no ponto mais baixo? (b) Essa velocidade aumenta, diminui ou permanece a mesma se a massa aumenta?

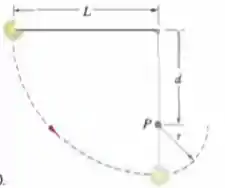
(Capítulo 8.4 – Exercício 5) Qual é a constante elástica de uma mola que armazena de energia potencial ao ser comprimida ?

(Capítulo 8.5 – Exercício 21) A corda da Fig. 8-36, de comprimento , possui uma bola presa em uma das extremidades e está fixa na outra extremidade. A distância da extremidade fixa a um pino no ponto é . A bola, inicialmente em repouso, é liberada com o fio na posição horizontal, como mostra a figura, e percorre a trajetória indicada pelo arco tracejado. Qual é a velocidade da bola ao atingir (a) o ponto mais baixo da trajetória e (b) o ponto mais alto depois que a corda encosta no pino?

(Capítulo 8.5 – Exercício 23) Em , uma bola de é atirada de uma torre com . Quanto é do sistema bola-Terra entre e (ainda em queda livre)?

(Capítulo 8.5 – Exercício 18) Um bloco de é liberado a partir do repouso de uma altura acima de uma mola vertical com constante elástica e massa desprezível. O bloco se choca com a mola e para momentaneamente depois de comprimir a mola . Qual é o trabalho realizado (a) pelo bloco sobre a mola e (b) pela mola sobre o bloco? (c) Qual é o valor de ? (d) Se o bloco fosse solto de uma altura acima da mola, qual seria a máxima compressão da mola?

(Capítulo 8.4 – Exercício 8) Na Fig. 8-31, um pequeno bloco de massa pode deslizar em uma pista sem atrito que forma um loop de raio . O bloco é liberado a partir do repouso no ponto , a uma altura acima do ponto mais baixo do loop. Qual é o trabalho realizado sobre o bloco pela força gravitacional quando o bloco se desloca do ponto para (a) o ponto e (b) o ponto mais alto do loop? Se a energia potencial gravitacional do sistema bloco-Terra é tomada como zero no ponto mais baixo do loop, qual é a energia potencial quando o bloco se encontra (c) no ponto , (d) no ponto e (e) no ponto mais alto do loop? (f) Se, em vez de ser simplesmente liberado, o bloco recebe uma velocidade inicial para baixo ao longo da pista, as respostas dos itens de (a) e (e) aumentam, diminuem ou permanecem as mesmas?

(Capítulo 8.5 – Exercício 15) Uma bola de gude de é lançada verticalmente para cima usando uma espingarda de mola. A mola deve ser comprimida de exatamente para que a bola alcance um alvo colocado acima da posição da bola de gude na mola comprimida. (a) Qual é a variação da energia potencial gravitacional do sistema bola de gude-Terra durante a subida de ? (b) Qual é a variação da energia potencial elástica da mola durante o lançamento da bola de gude? 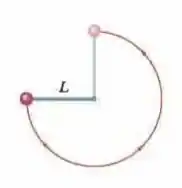(c) Qual é a constante elástica da mola?

(Capítulo 8.4 – Exercício 2) A Fig. 8-29 mostra uma bola de massa presa à extremidade de uma haste fina de comprimento e massa desprezível. A outra extremidade da haste é articulada, de modo que a bola pode se mover em uma circunfêrencia vertical. A haste é mantida na posição horizontal, como na figura, e depois recebe um impulso para baixo com força suficiente para que a bola passe pelo ponto mais baixo da circunferência e continue em movimento até chegar ao ponto mais alto com velocidade nula. Qual é o trabalho realizado sobre a bola pela força gravitacional do ponto inicial até (a) o ponto mais baixo, (b) o ponto mais alto, (c) o ponto à direita na mesma altura que o ponto inicial? Se a energia potencial gravitacional do sistema bola-Terra é tomada como zero no ponto inicial, determine o seu valor quando a bola atinge (d) o ponto mais baixo, (e) o ponto mais alto e (f) o ponto à direita na mesma altura que o ponto inicial. (g) Suponha que a haste tenha recebido um impulso maior e passe pelo ponto mais alto com uma velocidade diferente de zero. A variação do ponto mais baixo ao ponto mais alto é maior, menor ou a mesma que quando a bola chegava ao ponto mais alto com velocidade zero?

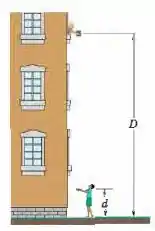
(Capítulo 8.4 – Exercício 1) Você deixa cair um livro de para uma amiga que está na calçada, a uma distância abaixo de você. Se as mãos estendidas da sua amiga estão a uma distância acima do solo (Fig. 8- 28), (a) qual é o trabalho realizado sobre o livro pela força gravitacional até o livro cair nas mãos da sua amiga? (b) Qual é a variação da energia potencial gravitacional do sistema livro-Terra durante a queda? Se a energia potencial gravitacional do sistema é considerada nula no nível do solo, qual é o valor de (c) quando você deixa cair o livro e (d) quando o livro chega às mãos da sua amiga? Suponha agora que o valor de seja ao nível do solo e calcule novamente (e) , (f) , (g) no ponto onde você deixou cair o livro e (h) no ponto em que o livro chegou às mãos da sua amiga.

(Capítulo 8.5 – Exercício 24) Um esquiador de parte do repouso a uma altura acima da extremidade de uma rampa para saltos de esqui (Fig. 8-35) e deixa a rampa fazendo um ângulo com a horizontal. Despreze os efeitos da resistência do ar e suponha que a rampa não tenha atrito. (a) Qual é a altura máxima do salto em relação à extremidade da rampa? (b) Se o esquiador aumentasse o próprio peso colocando uma mochila nas costas, seria maior, menor ou igual?

(Capítulo 8.5 – Exercício 27) A Fig. 8-34 mostra uma pedra de em repouso sobre uma mola. A mola é comprimida pela pedra. (a) Qual é a constante elástica da mola? (b) A pedra é empurrada mais para baixo e liberada. Qual é a energia potencial elástica da mola comprimida antes de ser liberada? (c) Qual é a variação da energia potencial gravitacional do sistema pedra-Terra quando a pedra se desloca do ponto onde foi liberada até a altura máxima? (d) Qual é essa altura máxima, medida a partir do ponto onde a pedra foi liberada?

(Capítulo 8.5 – Exercício 22) Um bloco de massa é deixado cair de uma altura sobre uma mola de constante elástica . Determine a variação máxima de comprimento da mola ao ser comprimida.

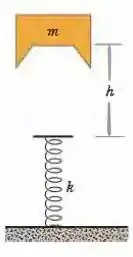
(Capítulo 8.5 – Exercício 29) Um bloco de massa é apoiado em uma mola em um plano inclinado sem atrito de ângulo (Fig. 8-42). (O bloco não está preso à mola.) A mola, de constante elástica , é comprimida e depois liberada. (a) Qual é a energia potencial elástica da mola comprimida? (b) Qual é a variação da energia potencial gravitacional do sistema bloco – Terra quando o bloco se move do ponto em que foi liberado até o ponto mais alto que atinge no plano inclinado? (c) Qual é a distância percorrida pelo bloco ao longo do plano inclinado até atingir a altura máxima?

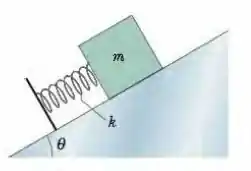
Figura 8-42 Problema 31

(Capítulo 8.5 – Exercício 26) Um pêndulo é formado por uma pedra de oscilando na extremidade de uma corda de de comprimento e massa desprezível. A pedra tem uma velocidade de ao passar pelo ponto mais baixo da trajetória. (a) Qual é a velocidade da pedra quando a corda forma um ângulo de com a vertical? (b) Qual é o maior ângulo com a vertical que a corda assume durante o movimento da pedra? (c) Se a energia potencial do sistema pêndulo-Terra é tomada sendo nula na posição mais baixa da pedra, qual é a energia mecânica total do sistema?

(Capítulo 8.5 – Exercício 25) Tarzan, que pesa , salta de um penhasco pendurado na extremidade de um cipó com de comprimento (Fig. 8-38). Do alto do penhasco até o ponto mais baixo da trajetória, ele desce . O cipó se romperá se a força exercida sobre ele exceder . (a) O cipó se rompe? Se a resposta for negativa, qual é a maior força a que é submetido o cipó? Se a resposta for afirmativa, qual é o ângulo que o cipó está fazendo com a vertical no momento em que se rompe?

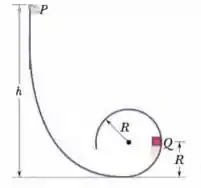
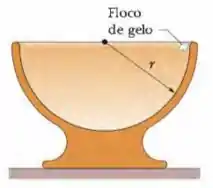
(Capítulo 8.4 – Exercício 3) Na Fig. 8-30, um floco de gelo de é liberado na borda de uma taça hemisférica com de raio. Não há atrito no contato do floco com a taça. (a) Qual é o trabalho realizado sobre o floco pela força gravitacional durante a descida do floco até o fundo da taça? (b) Qual é a variação da energia potencial do sistema floco-Terra durante a descida? (c) Se essa energia potencial é tomada como nula no fundo da taça, qual é seu valor quando o floco é solto? (d) Se, em vez disso, a energia potencial é tomada como nula no ponto onde o floco é solto, qual é o seu valor quando o floco atinge o fundo da taça? (e) Se a massa do floco fosse duplicada, os valores das respostas dos itens (a) e (d) aumentariam, diminuiriam ou permaneceriam os mesmos?

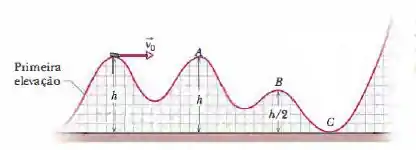
(Capítulo 8.4 – Exercício 4) Na Fig. 8-27, um carro de montanha-russa de massa atinge o cume da primeira elevação com uma velocidade a uma altura . O atrito é desprezível. Qual é o trabalho realizado sobre o carro pela força gravitacional entre este ponto e (a) o ponto , (b) o ponto e (c) o ponto ? Se a energia potencial gravitacional do sistema carro-Terra é tomada como nula em , qual é o seu valor quando o carro está (d) em e (e) em ? Se a massa é duplicada, a variação da energia potencial gravitacional do sistema entre os pontos e aumenta, diminui ou permanece a mesma?

Um disco de plástico de 75 g é arremessado de um ponto 1,1 m acima do solo, com uma velocidade escalar de 12 m/s. Quando o disco atinge uma altura de 2, 1 m, sua velocidade é 10,5 m/s. Qual é a redução da Emec do sistema disco-Terra devido ao arrasto do ar?

Na Fig. 8-50, um bloco de é acelerado a partir do repouso por uma mola comprimida de constante elástica . O bloco deixa a mola no seu comprimento relaxado e se desloca em um piso horizontal com um coeficiente de atrito cinético . A força de atrito para o bloco em uma distância . Determine (a) o aumento de energia térmica do sistema bloco-piso, (b) a energia cinética máxima do bloco e ( c) o comprimento da mola quando estava comprimida.

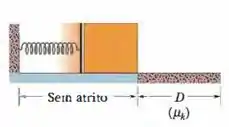
Figura 8-50 Problema 53.

Quando um besouro salta-martim está deitado de costas, pode pular encurvando bruscamente o corpo, o que converte a energia armazenada em um músculo em energia mecânica, produzindo um estalo audível. O videoteipe de um desses pulos mostra que um besouro de massa se desloca na vertical durante um salto e consegue atingir uma altura máxima . Qual é o valor médio, durante o salto, (a) do módulo da força externa exercida pelo piso sobre as costas do besouro e (b) do módulo da aceleração do besouro em unidades de g?

Na Fig. 8-40, um bloco de massa desliza para baixo, a partir do repouso, percorre uma distância em um plano inclinado de ângulo e se choca com uma mola de constante elástica . Quando o bloco para momentaneamente, a mola fica comprimida . Quais são (a) a distância e (b) a distância entre o ponto do primeiro contato do bloco com a mola e o ponto onde a velocidade do bloco é máxima?

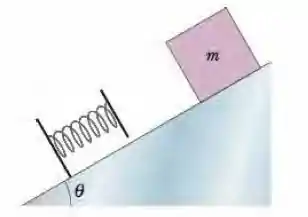
Figura 8-40 Problema 35

(Cap. 8 – Ex. 56) Um pacote de começa a subir um plano inclinado de com uma energia cinética de . Que distância ele percorre antes de parar, se o coeficiente de atrito cinético entre o pacote e o plano é ?

Um collie arrasta a caixa de dormir em um piso, aplicando uma força horizontal de . O módulo da força de atrito cinético que age sobre a caixa é. Quando a caixa é arrastada por uma distância de , quais são (a) o trabalho realizado pela força do cão e (b) o aumento de energia térmica da caixa e do piso?

Uma partícula pode deslizar em uma pista com extremidades elevadas e uma parte central plana, como mostra a Fig. 8-56. A parte plana tem um comprimento . Os trechos curvos da pista não possuem atrito, mas na parte plana o coeficiente de atrito cinético é . A partícula é liberada a partir do repouso no ponto , que está a uma altura . A que distância da extremidade esquerda da parte plana a partícula finalmente para?

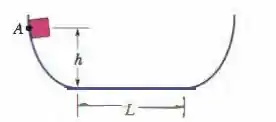
Figura 8-56 Problema 65.

O cabo do elevador de da Fig. 8-54 se rompe quando o elevador está parado no primeiro andar, onde o piso se encontra a uma distância acima de uma mola de constante elástica . Um dispositivo de segurança prende o elevador aos trilhos laterais, de modo que uma força de atrito constante de passa a se opor ao movimento. (a) Determine a velocidade do elevador no momento em que se choca com a mola. (b) Determine a máxima redução do comprimento da mola (a força de atrito continua a agir enquanto a mola está sendo comprimida). (c) Determine a distância que o elevador sobe de volta no poço. (d ) Usando a lei de conservação da energia, determine a distância total aproximada que o elevador percorre antes de parar. (Suponha que a força de atrito sobre o elevador seja desprezível quando o elevador está parado.)

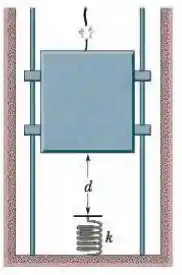
Figura 8-54 Problema 63.

(Capítulo 8.5 – Exercício 31) Na Fig. 8-40, um bloco de massa é liberado a partir do repouso em um plano inclinado sem atrito de ângulo . Abaixo do bloco há uma mola que pode ser comprimida por uma força de . O bloco para momentaneamente após comprimir a mola . (a) Que distância o bloco desce ao longo do plano da posição de repouso inicial até o ponto em que para momentaneamente? (b) Qual é a velocidade do bloco no momento em que entra em contato com a mola?

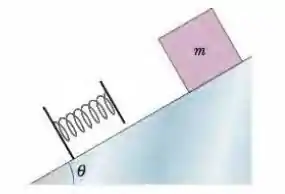
Figura 8-40 Problema 29

Na Fig. 8-51, um bloco de massa desliza de encontro a uma mola de constante elástica . O bloco para após comprimir a mola . O coeficiente de atrito cinético entre o bloco e o piso é. Enquanto o bloco está em contato com a mola e sendo levado ao repouso, determine (a) o trabalho realizado pela mola e (b) o aumento da energia térmica do sistema bloco-piso. (c) Qual é a velocidade do bloco imediatamente antes de se chocar com a mola?

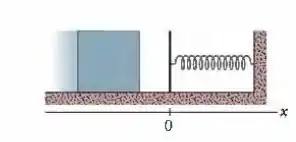
Figura 8-51 Problema 55.

Um menino está inicialmente sentado no alto de um monte hemisférico de gelo de raio . Ele começa a deslizar para baixo com uma velocidade inicial tão pequena que pode ser desprezada (Fig. 8-45). Suponha que o atrito com o gelo seja desprezível. Em que altura o menino perde contato com o gelo?

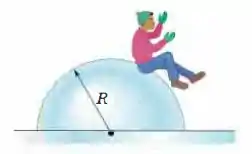
Figura 8-45 Problema 34

(Cap. 8 – Ex. 47) Um urso de escorrega, a partir do repouso, para baixo em um tronco de pinheiro, movendo-se com uma velocidade de imediatamente antes de chegar ao chão. (a) Qual é a variação da energia potencial gravitacional do sistema urso-Terra durante o deslizamento? (b) Qual é a energia cinética do urso imediatamente antes de chegar ao chão? (c) Qual é a força de atrito média que age sobre o urso enquanto está escorregando?

Na Fig. 8 - 52, um bloco desliza ao longo de uma pista, de um nível para outro mais elevado, passando por um vale intermediário. A pista não possui atrito até o bloco atingir o nível mais alto, onde uma força de atrito para o bloco depois que ele percorre uma distância . A velocidade inicial do bloco é a diferença de altura é e é . Determine o valor de.

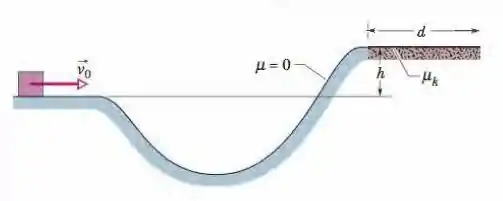
Figura 8-52 Problema 57.

Um operário empurra um caixote de , com velocidade constante, por , ao longo de um piso plano, com uma força orientada abaixo da horizontal. Se o coeficiente de atrito cinético entre o bloco e o piso é , quais são (a) o trabalho realizado pelo operário e (b) o aumento da energia térmica do sistema bloco-piso?

(Cap. 8 – Ex. 5) Duas meninas estão disputando um jogo no qual tentham acertar uma pequena caixa no chão com uma bola de gude lançada por um canhãao de mola montado em uma mesa. A caixa está a uma distância horizontal da borda da mesa; veja a Fig. 8-46. Lia comprime a mola , mas o centro da bola de gude cai antes do centro da caixa. De quanto Rosa deve comprimir a mola para acertar a caixa? Suponha que o atrito da mola e da bola com o canhãao seja desprezível.

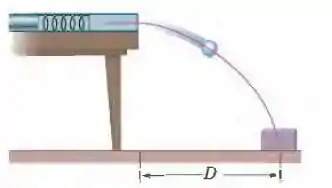
Figura 8-46 Problema 36

Uma partícula de tem coordenadas (, ) e uma partícula de tem coordenadas (, ). Ambas estão em um plano horizontal. Em que coordenada (a) e (b) deve ser posicionada uma terceira partícula de para que o centro de massa do sistema de três partículas tenha coordenadas (, )?

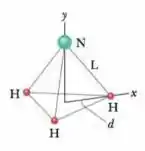
Na molécula de amônia () da Fig. 9-40, três átomos de hidrogênio (H) formam um triângulo equilátero, com o centro do triângulo a uma distância de cada átomo de hidrogênio. O átomo de nitrogênio (N) está no vértice superior de uma pirâmide, com os três átomos de hidrogênio formando a base. A razão entre as massas de nitrogênio e do hidrogênio é e a distância nitrogênio-hidrogênio é . Quais são as coordenadas (a) e (b) do centro de massa da molécula?

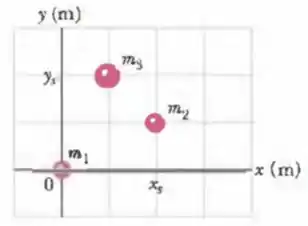
A Fig. 9-35 mostra um sistema de três partículas de massas , e . As escalas do gráfico são definidas por e . Quais são (a) a coordenada e (b) a coordenada do centro de massa do sistema? (c) Se aumenta gradualmente, o centro de massa do sistema se aproxima de , se afasta de ou permanece onde está?

Quais são (a) a coordenada e (b) a coordenada do centro de massa da placa homogênea da Fig. 9-38 se ?

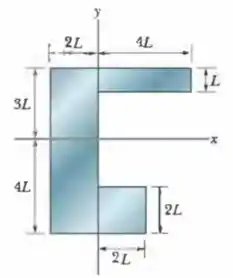
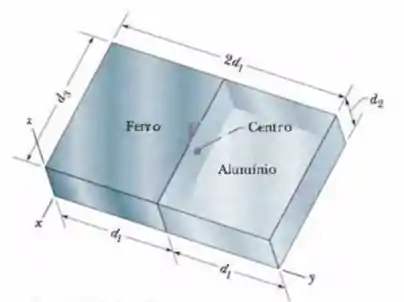
A Fig. 9-36 mostra uma placa composta de dimensões , e . Metade da placa é feita de alumínio (massa especifica = ) e a outra metade de ferro (massa especifica = ). Determine (a) a coordenada , (b) a coordenada e (c) a coordenada do centro de massa da placa.

Dois patinadores, um de e outro de , estão em uma pista de gelo e seguram as extremidades de uma base de de comprimento e massa desprezível. Os patinadores se puxam ao longo da haste até se encontrarem. Qual é a distância percorrida pelo patinador de ?

Uma lata tem uma massa de , uma altura de e contém de refrigerante (Fig. 9-42). Pequenos furos são feitos na base e na tampa (com perda de massa desprezível) para drenar o refrigerante. Qual é a altura do centro de massa da lata e seu conteúdo (a) inicialmente e (b) após a lata perder todo o refrigerante? (c) O que acontece com enquanto o refrigerante está sendo drenado? (d) Se é a altura do refrigerante que ainda resta na lata em um dado instante, determine o valor de no instante em que o centro de massa atinge o ponto mais baixo.