Tipler, Mosca; Física Para Cientistas e Engenheiros; 6ª Ed. - Capítulo 7, Seção 1, Questão 38.
(Cap 7 – Ex 38) Um bloco de desliza ao longo de uma superfície horizontal sem atrito com uma velocidade de (Figura 7-41). Após deslizar por uma distância de , o bloco faz uma suave transição para uma rampa sem atrito inclinada a um ângulo de 40° com a horizontal. Qual a distância, ao longo da rampa, que o bloco percorre até atingir momentaneamente o repouso?
Passo 1
Olá, querido! Tá bem?
Então, o que ele diz é que temos um bloco de com velocidade constante . Ele anda sobre um parte horizontal e depois chega numa rampa, onde ele atinge uma altura máxima e para.
Aí o que ele quer saber é o quanto esse carinha andou sobre a rampa até parar.
Vamos pensar no movimento do bloco em relação a energia dele, ok? Temos 3 momentos: quando o bloco está no começo da parte horizontal, no pé da rampa antes de subir e a altura máxima. Se liga no esqueminha:
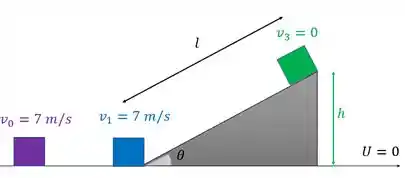
Quando ele anda na parte horizontal, como não há atrito (como diz o enunciado diz), a velocidade não muda. Por isso . E na altura máxima a velocidade dele é nula, logo .
E percebe que na altura , temos o referencial de energia potencial gravitacional .
Como no ponto 1 e 2 temos a mesma altura e velocidade, a gente pode comparar um desses dois pontos com o ponto 3, e descobrir a distância percorrida pelo bloco. Comparar como? Usando a conservação de energia mecânica! Vamos ver como fazer isso!
Passo 2
Como não há atrito nem na parte horizontal e nem na rampa, podemos dizer que não há forças externas realizando trabalho sobre nosso bloquinho. E por isso, a energia mecânica do sistema é constante. Podemos então comparar o ponto 1 e o 3 da seguinte forma:
Ou seja, a energia mecânica nesses dois pontos é igual.
Como a energia mecânica no caso do nosso bloquinho é soma da energia potencial gravitacional e a energia cinética , podemos escrever:
Agora, vamos as análises. Como no ponto final a velocidade é nula, e como a energia cinética é proporcional a velocidade, a energia cinética final vai ser nula . E como no ponto 1 a gente está em , vamos ter energia potencial gravitacional nula .
Substituindo essas duas coisas na nossa equação:
Passo 3
Agora é substituir na relação expressa anteriormente, as fórmulas relativas a energia potencial gravitacional final e a energia cinética inicial :
Mas o que é esse da fórmula? Bem, o nada mais é do que a altura máxima que o bloco atinge na rampa. Só que a gente quer o certo? Então vamos relacionar e usando trigonometria no triângulo da nossa figura. Podemos dizer que
Substituindo isso na nossa equação acima:
Isolando quem a gente quer:
Basta substituir os valores numéricos:
Resposta
O bloco percorre uma distância igual a .