Listas de Estudos pra Prova - Tipler Vol 1 - 6°ed de Física 1 da UTFPR - Rotação e Momento Angular

(Cap 9 – Ex 73) No sistema do problema 71, se a prateleira (sem atrito) for ajustada com uma inclinação, qual deve ser essa inclinação para que os blocos se movam com uma rapidez constante?

(Cap 9 – Ex 34) Qual é a rapidez angular da Terra, em radianos por segundo, na rotação em torno de seu eixo?

(Cap 9 – Ex 59) Um cilindro de , cujo raio é de , inicialmente em repouso, pode girar livremente em torno de seu eixo. Uma corda de massa desprezível é enrolada em torno dele e puxada com uma força de . Supondo que a corda não escorregue, determine (a) o torque exercido pela corda sobre o cilindro, (b) a aceleração angular do cilindro e (c) a rapidez angular do cilindro após .

(Capítulo 9.1 – Exercício 33) Um ciclista acelera uniformemente a partir do repouso. Após , as rodas completam . (a) Qual é a aceleração angular das rodas? (b) Qual é a rapidez angular das rodas ao final dos ?

(Capítulo 9.1 – Exercício 72) No sistema do problema 71, o bloco de é largado do repouso. (a) Determine a rapidez do bloco depois de ele ter caído uma distância de . (b) Qual é a rapidez angular da polia neste instante?

(Cap 9 – Ex 36) Uma bicicleta tem rodas de de diâmetro. O ciclista acelera a partir do repouso, com aceleração constante, até , em . Qual é a aceleração angular das rodas?

(Cap 9 – Ex 32) Uma roda-gigante de de raio completa uma volta a cada . (a) Qual é a sua rapidez angular (em radianos por segundo)? (b) Qual é a rapidez linear de um passageiro? (c) Qual é a aceleração de um passageiro?

(Capítulo 9.1 – Exercício 28) Uma partícula se move com uma rapidez constante de em um círculo de de raio. (a) Qual é a sua rapidez angular em radianos por segundo em relação ao centro do círculo? (b) Quantas voltas ela dá em ?

(Capítulo 9.1 – Exercício 71) O sistema mostrado na figura consiste em um bloco de colocado sobre uma prateleira horizontal sem atrito. Este bloco está preso a um cordão que passa por uma polia e tem sua outra extremida presa a um bloco pendente . A polia é um disco uniforme de de raio e de massa. Determine a aceleração de cada bloco e as tensões no cordão.

(Capítulo 9.1 – Exercício 35) Uma roda varre em ao ser levada ao repouso com aceleração angular constante. Determine a rapidez angular inicial da roda ao começar a ser freada.

(Capítulo 9.1 – Exercício 29) Uma roda, partindo do repouso, gira com aceleração angular constante de . Após da partida: (a) Qual é sua rapidez angular? (b) Qual é o ângulo varrido pela roda? (c) Quantas voltas ela completou? (d) Qual é a rapidez linear e qual é a magnitude da aceleração linear de um ponto distante do eixo de rotação?

Para ligar um cortador de grama, você deve puxar uma cordinha que está enrolada ao longo do perímetro de um volante. Depois de você puxar a corda por , o volante está girando a revoluções por segundo quando a cordinha se desprende. Esta tentativa de ligar o cortador não funciona, no entanto, e o volante acaba por parar após do desprendimento da cordinha. Suponha aceleração constante, tanto durante a puxada da cordinha quanto durante o freamento do volante. (a) Determine a aceleração angular média durante os em que a cordinha está sendo puxada e durante os do fretamento do volante. (b) Qual é a maior rapidez angular atingida pelo volante? (c) Determine a razão entre o número de voltas realizadas na primeira etapa e o número de voltas realizadas na segunda etapa.

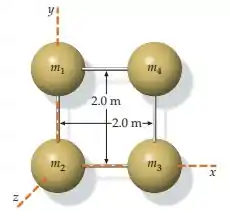
(Capítulo 9.1 – Exercício 41) Quatro partículas, uma em cada um dos cantos de um quadrado de de lado, estão ligadas por barras sem massa (figura 9-45). As massas das partículas são e . Determine o momento de inércia do sistema em relação ao eixo .

(Capítulo 9.1 – Exercício 30) Uma mesa giratória, girando a , é levada ao repouso em 26 s. Supondo constante a aceleração angular, encontre (a) a aceleração angular. Durante esses , determine (b) a rapidez angular média e (c) o deslocamento angular em número de voltas.

(Capítulo 9.1 – Exercício 61) Um pêndulo consistindo em um fio de comprimento preso a uma bolinha de massa oscila em um plano vertical. Quando o fio forma um ângulo com a vertical, (a) calcule a aceleração tangencial da bolinha, usando . (b) Qual é o torque exercido em relação ao ponto pivô? (c) Mostre que , com , fornece a mesma aceleração tangencial encontrada na parte (a).

(Capítulo 9.1 – Exercício 31) Um disco de 12 cm de raio, que começa a girar em torno de seu eixo em , gira com uma aceleração angular constante de . Em , (a) qual é a rapidez angular do disco e (b) quais são as componentes tangencial e centrípeta da aceleração de um ponto na borda do disco?

(Capítulo 9.1 – Exercício 60) Uma roda de amolar está inicialmente em repouso. Um torque externo constante de é aplicado sobre a roda durante , imprimindo à pedra uma rapidez angular de . O torque externo é então retirado, e a roda atinge o repouso depois. Determine (a) o momento de inércia da roda e (b) o torque causado pelo atrito, suposto constante.

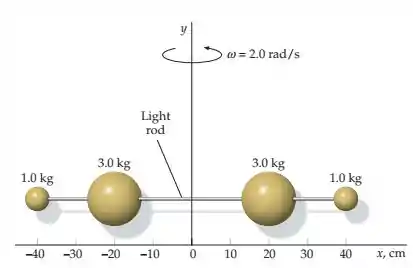
(Capítulo 9.1 – Exercício 64) As partículas da figura estão ligadas por uma barra muito leve. Elas giram em torno do eixo a . (a) Determine a rapidez de cada partícula e utilize esses valores para calcular a energia cinética do sistema diretamente a partir de . (b) Determine o momento de inérica em relação ao eixo , calcule a energia cinética a partir de e compare seu resultado com o resultado da parte (a).

(Capítulo 9.1 – Exercício 37) A fita em um videocassete VHS padrão tem um comprimento total de , o suficiente para operar durante . Quando no início, o carretel cheio tem um raio externo de e um raio interno de . Em algum momento da operação, os dois carretéis têm a mesma rapidez angular. Calcule esta rapidez angular em radianos por segundo e em revoluções por minutos. Dica: Entre os dois carretéis, a fita corre com rapidez constante.

(Capítulo 9.1 – Exercício 74) No sistema mostrado na figura, o bloco de está sobre a prateleira horizontal. O coeficiente de atrito cinético entre a prateleira e o bloco é . O bloco está preso a um cordão que passa pela polia e tem sua outra extremidade presa a um bloco pendente de . A polia é um disco uniforme de de raio e de massa. Determine a aceleração de cada bloco e as tensões no cordão.

(Cap 10 – Ex 64) Se, no sistema do Problema 64, , , , e o maior ângulo entre a barra e a vertical após a colisão é , determine a rapidez da partícula antes do impacto.

(Cap 10 – Ex 49) Você está de pé sobre uma plataforma sem atrito que está girando com uma rapidez angular de . Seus braços estão esticados para fora, e você segura um peso em cada mão. O momento de inércia do conjunto formado por você, os pesos estendidos e a plataforma é . Quando você puxa os pesos para perto do seu corpo, o momento de inércia é reduzido para . (a) Qual é a rapidez angular final da plataforma? (b) Qual é a variação na energia cinética do sistema? (c) De onde veio esse aumento de energia?

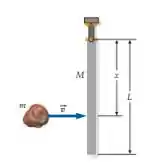
(Cap 10 – Ex 63) A Figura 10-53 mostra uma barra fina e uniforme, de comprimento e massa , articulada na extremidade superior. A barra, que está inicialmente em repouso, é atingida por uma partícula de massa no ponto abaixo da articulação. Suponha que a partícula grude na barra. Qual deve ser a rapidez da partícula, de forma que após a colisão o maior ângulo entre a barra e a vertical seja ?

(Capítulo 9.1 – Exercício 76) O sistema da figura 9-57 é largado do repouso quando o bloco de está acima da prateleira. A polia é um disco uniforme de com um raio de . Justo antes de o bloco de atingir a prateleira, determine (a) sua rapidez, (b) a rapidez angular da polia e (c) a tensão nos fios. (d) Determine o tempo de queda do bloco de . Suponha que o fio não deslize na polia.

(Cap 10 – Ex 37) Uma partícula de se move diretamente para o leste com uma rapidez constante de , ao longo de uma linha oeste-leste. (a) Qual é sua quantidade de movimento angular (incluindo a orientação) em relação a um ponto que está a ao norte da linha? (b) Qual é sua quantidade de movimento angular (incluindo a orientação) em relação a um ponto que está a ao sul da linha? (a) Qual é sua quantidade de movimento angular (incluindo a orientação) em relação a um ponto que está a diretamente a leste da linha?

(Cap 10 – Ex 28) Calcule o torque, em relação à origem, da força gravitacional que atua sobre uma partícula de massa localizada em , e mostre que este torque é independente da coordenada .

(Cap 10 – Ex 51) Um pesado disco de plástico está montado sobre mancais sem atrito no eixo vertical que passa pelo seu centro. O disco tem raio e massa . Uma barata (massa ) está sobre o disco, a uma distância de do centro. Inicialmente, tanto o disco quanto a barata estão em repouso. A barata começa, então, a caminhar ao longo de uma trajetória circular concêntrica ao eixo do disco, à distância constante de do eixo. Se a rapidez da barata em relação ao disco é , qual é a rapidez da barata em relação à sala?

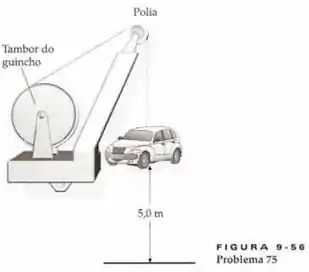
(Capítulo 9.1 – Exercício 75) Um carro de está sendo retirado da água por um guincho. No momento em que o carro está acima da água, a caixa de engrenagens quebra e o tambor do guincho gira livremente enquanto o carro cai. Durante a queda do carro, não existe deslizamento entre a corda (sem massa), a polia e o tambor. O momento de inércia do tambor do guincho é e o momento de inércia da polia é . O raio do tambor é e o raio da polia é . Suponha o carro partindo do repouso. Determine a rapidez com que ele atinge a água.

(Cap 9 – Ex 110) Um disco uniforme de tem um raio de e gira livremente em torno de seu eixo. Um cordão, enrolado em volta do disco, é puxado com uma força de . (a) Qual é o torque exercido por esta força em relação ao eixo de rotação? (b) Qual é a aceleração angular do disco? (c) Se o disco parte do repouso, qual é sua rapidez angular após ? (d) Qual é a energia cinética após os ? (e) Qual é o deslocamento angular do disco durante os ? (f) Mostra que o trabalho realizado pelo torque, , é igual à energia cinética.

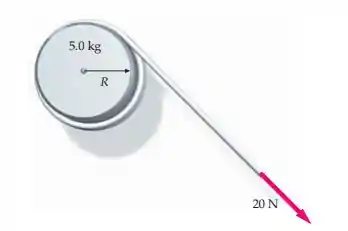
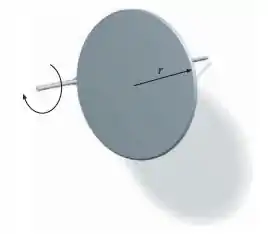
(Cap 9 – Ex 117) Um disco uniforme de raio e massa gira em torno de um eixo horizontal paralelo ao seu eixo de simetria e que passa por um ponto de seu perímetro, de forma a poder oscilar livremente em um plano vertical. Ele é largado do repouso, com seu centro de massa à mesma altura do pivô. (a) Qual é a rapidez angular do disco, quando seu centro de massa está diretamente abaixo do pivô? (b) Qual é a força exercida pelo pivô sobre o disco neste momento?

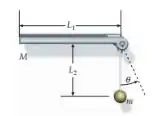
(Cap 10 – Ex 68) Uma barra uniforme, de comprimento igual a e massa igual a , está presa a uma dobradiça de massa desprezível em uma das extremidades e é livre para girar no plano vertical (Figura 10-55). A barra é largada do repouso na posição mostrada. Uma partícula, de massa , está suspensa da dobradiça por um fio fino de comprimento igual a . A partícula gruda da barra quando as duas encostam e após a colisão, a barra continua a gira até . (a) Determine . (b) Quanta energia é dissipada na colisão?

(Cap 9 – Ex 101) Uma bola de boliche, de massa e raio , é lançada de forma que, ao atingir o piso, está se movendo horizontalmente com um rapidez , sem girar. Ela desliza uma distância durante um tempo antes de começar a rolar sem deslizar. (a) Se é o coeficiente de atrito cinético entre a bola e o piso, determine , e a rapidez final da bola. (b) Determine a razão entre a energia cinética final e a energia cinética inicial da bola. (c) Determine , e para e .