Listas de Estudos pra Prova - Halliday Vol 1 - 8°ed de Física 1 da UTFPR - Vetores

(Capítulo 3.4 – Exercício 5) O objetivo de um navio échegar a um porto situado ao norte do ponto de partida, mas uma tempestade inesperada o leva para um local situado a leste do ponto de partida. (a) Que distância o navio deve percorrer e (b) qual o rumo deve tomar para chegar ao destino?

Se e , determine .

(Capítulo 3.4 – Exercício 2) Expresse os seguintes ângulos em radianos: (a) ; (b) ; (c) . Converta os seguintes ângulos para graus: (d) ; (e) ; (f) .

(Capítulo 3.6 – Exercício 9)

(a) Determine a soma , em termos de vetores unitários, para e . Determine (b) o módulo e (c) a orientação de .

Três vetores são dados por , e . Determine (a) , (b) e

Se é somado a , o resultado é um vetor no sentido do semi-eixo y positivo, com um módulo igual ao de . Qual o módulo de ?

(Capítulo 3.4 – Exercício 4) Na Fig. 3-27, uma máquina pesada é erguida com o auxílio de uma rampa que faz um ângulo com a horizontal, na qual a máquina percorre uma distância . (a) Qual é a distância vertical percorrida pela máquina? (b) Qual é a distância horizontal percorrida pela máquina?

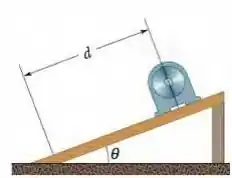
Os vetores e da Fig. 3-28 têm o mesmo módulo, , e os ângulos mostrados na figura são e . Determine as componentes (a) e (b) da soma vetorial dos dois vetores, (c) o módulo de e (d) o ângulo que faz com o semieixo positivo.

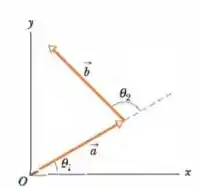
(Capítulo 3.4 – Exercício 6) Um vetor deslocamento no plano tem de comprimento e faz um ângulo com o semieixo positivo, como mostra a Fig 3-26. Determine (a) a componente e (b) a componente do vetor.

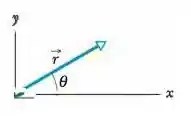
Dois vetores são dados por e . Determine, em termos de vetores unitários, (a) ; (b) ; (c) um terceiro vetor, , tal que

(Capítulo 3.4 – Exercício 1) A componente do vetor é e a componente é . (a) Qual é o módulo de ? (b) Qual é o ângulo entre a orientação de e o semieixo positivo?

(Capítulo 3.6 – Exercício 8) Um carro viaja para leste, para o norte e em uma direção a leste do norte. Desenhe o diagrama vetorial e determine (a) o módulo e (b) o ângulo do deslocamento do carro em relação ao ponto de partida.

(Capítulo 3.4 – Exercício 7) As dimensões de uma sala são (altura) X X . Uma mosca parte de um canto da sala e pousa em um canto diagonalmente oposto. (a) Qual é o módulo do deslocamento da mosca? (b) A distância percorrida pode ser menor que este valor? (c) Pode ser maior? (d) Pode ser igual? (e) Escolha um sistema de coordenadas apropriado e expresse as componentes do vetor deslocamento em termos de vetores unitários. (f) Se a mosca caminhar, em vez de voar, qual é o comprimento do caminho mais curto para o outro canto? (Sugestão: o problema pode ser resolvido sem fazer cálculos complicados. A sala é como uma caixa; desdobre as paredes para representá-las em um mesmo plano antes de procurar uma solução.)

(Capítulo 3.6 – Exercício 11) Uma pessoa deseja chegar a um ponto que está a de sua localização atual, em uma direção ao norte do leste. As ruas por onde pode passar são todas na direção norte-sul ou na direção leste-oeste. Qual é a menor distância que a pessoa precisa percorer para chegar ao destino?

(Capítulo 3.6 – Exercício 10) Uma pessoa caminha da seguinte forma: para o norte, para o oeste e para o sul. (a) Desenhe o diagrama vetorial que representa este movimento. (b) Que distância e (c) em que direção voaria um pássaro em linha reta do mesmo ponto de partida ao mesmo ponto de chegada?

(Capítulo 3.4 – Exercício 3) Quais são (a) a componente e (b) a componente de um vetor do plano que faz um ângulo de no sentido anti-horário com o semieixo positivo e tem um módulo de ?

Uma formiga, enlouquecida pelo Sol em um dia quente, sai correndo em um plano . As componentes ( e ) de quatro corridas consecutivas em linha reta são as seguintes, todas em centímetros: , , ; . O deslocamento resultante das quatro corridas tem componentes . Determine (a) e (b) . Determine (c) o módulo e (d) o ângulo (em relação ao semieixo positivo) do deslocamento total.

(Capítulo 3.6 – Exercício 11) Para os vetores e , determine (a) em termos de vetores unitários e em termos (b) do módulo e (c) do ângulo (em relação a ). Determine (d) em termos de vetores unitários e em termos (e) do módulo e (f) do ângulo.

(a)Qual é a soma dos quatro vetores a seguir em termos de vetores unitários? (b) Para essa soma, quais são (b) o módulo, (c) o ângulo em graus, e (d) o ângulo em radianos?

Os três vetores na Fig. 3-33 têm módulos , e ; Determine (a) a componente e (b) a componente de ; (c) a componente e (d) a componente de ; (e) a componente e (f) a componente de . Se , quais são os valores de (g) e (h) ?