2CH de Física 2 da UFRJ - 2018.2

Numa região em que a pressão atmosférica vale , a maior altura em que um certo óleo de densidade pode ser elevado por sucção, supondo é:

Uma certa quantidade de gás ideal contida no recipiente de um manômetro de tubo aberto está inicialmente a uma temperatura , quando a pressão manométrica vale . A pressão atmosférica local vale O gás é aquecido a volume constante, até atingir uma temperatura , quando a pressão manométrica atinge o dobro da inicial. Qual a relação entre as temperaturas?

A figura mostra o desenho de um túnel cavado por um cachorro da savana. A geometria e o posicionamento da entrada e da saída do túnel, correspondentes a dois buracos, asseguram que o vento que sopra sobre o buraco número 2 sempre terá uma velocidade mais baixa do que aquele que sopra sobre o buraco número 1. Podemos afirmar que:

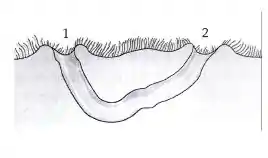
1. O ar flui através do túnel, do buraco 2 para o buraco 1, ventilando o ambiente.
2. O ar flui através do túnel, do buraco 1 para o buraco 2, ventilando o ambiente.
3. O ar dentro do túnel não é afetado. Os dois buracos servem apenas para rota de fuga do animal.
4. Nada se pode afirmar com as informações disponíveis.

Um pêndulo é formado por um fio ideal de comprimento e uma partícula de massa . Ele é afastado de um ângulo no sentido positivo da posição de equilíbrio e abandonado a partir do repouso, realizando pequenas oscilações que podem ser tratadas como harmônicas simples. Sua energia cinética como função do tempo é dada pela função:

a)

b)

c)

d)

Num certo processo reversível, uma certa quantidade de um gás ideal é aquecida isotermicamente até que seu volume dobre. Num outro processo, este irreversível, a mesma quantidade de gás, partindo do mesmo estado de equilíbrio térmico inicial, sofre várias mudanças, mas atinge o mesmo estado de equilíbrio térmico final do caso reversível. Sejam as variações da energia interna e da entropia no processo reversível. Analogamente, sejam as variações da energia interna e da entropia no processo irreversível. Podemos afirmar que:

Considere o ciclo de Stirling, funcionando como refrigerador, para o qual as etapas são isotérmicas e as etapas são isovolumétricas. São conhecidas as temperaturas máximas e mínima e o razão entre o maior e o menor volume. Suponha que a substância de trabalho é um gás ideal com n moles e capacidade térmica molar a volume constante

(a) Esboce o diagrama correspondente a este ciclo, deixando claro cada uma das etapas.

(b) Determine o calor trocado e o trabalho realizado pelo gás em cada um dos quatro processos do ciclo.

(c) Qual a variação da entropia em cada ciclo?

Enquanto um trem se afasta com velocidade constante de uma estação, num dia sem vento, da janela de um dos últimos vagões uma moça se despede do namorado que ficou na plataforma. A locomotiva, que vai à frente, apita com uma frequência . Seja a frequência percebida pela moça e a frequência percebida pelo rapaz. Podemos afirmar que:

A posição de uma partícula é dada por , onde é dado em segundos. Seja o primeiro instante após em que a partícula passa pela origem e seja sua velocidade neste instante. Podemos afirmar que:

Uma mola ideal de constante elástica está fixada ao solo, mantendo-se na posição vertical. Ela tem na sua parte superior um prato, de massa desprezível. O comprimento da mola nesta situação inicial, sem deformação, vale . Uma pessoa segura um objeto de massa encostada no prato e o abandona. O objeto fica nele grudado, passando este sistema massa+mola a oscilar verticalmente.

a) Determine a posição vertical yeq em relação ao solo em torno da qual o sistema irá oscilar.

b) Tomando este ponto como nova origem, escreva a expressão para a deformação da mola numa posição qualquer.

c) Obtenha a equação diferencial para que governa este movimento de oscilação.

d) Considerando o instante em que o objeto é abandonado sobre o prato, e usando a nova origem introduzida no item b), escreva as condições iniciais deste movimento de oscilação.

e) Escreva a função horária que descreve este movimento na forma , deixando claro as expressões para a frequência angular, para a amplitude, e para a constante de fase.